What’s Sin A cos A and tan A for a triangle with the opposite of 15 and a hypotenuse of 39?
3 Answers
Explanation:
First you have to know some formulas. First, I will show how to find a leg of a triangle.
Then turn this around and get
So now you plug in the numbers.
And after simplifying,
And
Now
Explanation:
"find the third side (adjacent) using "color(blue)"Pythagoras' theorem"
rArr"adjacent "=sqrt(39^2-15^2)=36
rArrsinA="opposite"/"hypotenuse"=15/39=5/13
cosA="adjacent"/"hypotenuse"=36/39=12/13
tanA="opposite"/"adjacent"=15/36=5/12
Explanation:
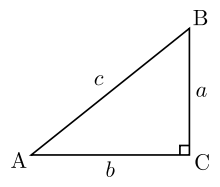
Given :
As per Pythagoras theorem,
