Question

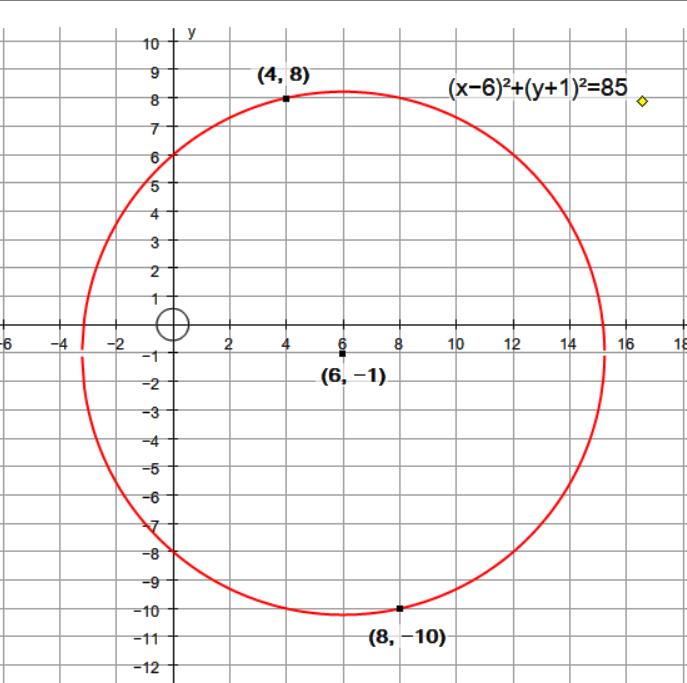
What's the equation of the circle? The end points of the diameter (4,8) and (8,-10)

Answer 1

`(x-6)^2+(y+1)^2=85`

Explanation:

Given diameter end points `(4,8)` and `(8,-10)`
the center of the circle must be at `((4+8)/2,(8-10)/2)=(6,-1)`

The square of the radius can be calculated using the Pythagorean Theorem from this center and the point `(4,8)` as
`color(white)("XXX")r^2=(6-4)^2 +(-1-8)^2=4+81=85`

A congruent circle with center `(0,0)` would have an equationof the form:
`color(white)("XXX")(hatx)^2+(haty)^2=85`

To shift this circle to the required center `(6,-1)`
we need to replace `hatx` with `x-6`
and `haty` with `y+1`

creating the required relation:
`color(white)("XXX")(x-6)^2+(y+1)^2=85`

Answer 2

Equation of the circle is `(x – 6)^2 + (y +1 )^2 = 85`

Explanation:

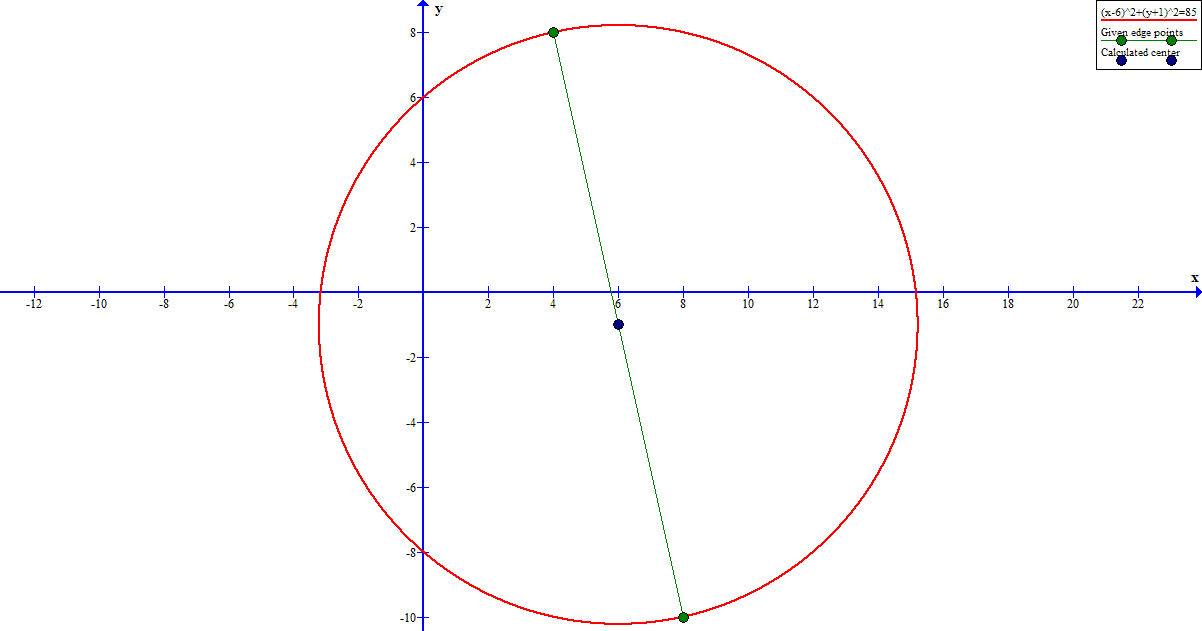
The end points of diameter are `(4,8), (8,-10)`

The center-radius form of the circle equation is

`(x – h)^2 + (y – k)^2 = r^2`, with the center being at the point

`(h, k)` and the radius being `r`.

The centre is the mid point of diameter.

So centre is `(4+8)/2,(8-10)/2 or (6,-1)`

`(4,8) and (6,-1)` are the end points of radius `r`.

Distance formula is `D= sqrt ((x_1-x_2)^2+(y_1-y_2)^2`

`:.r^2=(4-6)^2+(8+1)^2 = 85` . Equation of the circle is

`(x – 6)^2 + (y +1 )^2 = 85`

graph{(x-6)^2+(y+1)^2=85 [-38.9, 38.88, -19.45, 19.44]}

[Ans]

Answer 3

`(x-6)^2+(y+1)^2=85`

Explanation:

If `(4,-8)` and `(8,-10)` are the end points of the diameter, then the coordinates of the mid point of the diameter are given by:

`((x_1+x_2)/2,(y_1_y_2)/2)`

`((4+8)/2,(8+(-10))/2)`

`(6,-1)`

These are therefore the coordinates of the centre of the circle.

Using the distance formula, we can find the length of the diameter.

The distance formula states that. Distance `bbd` is:

`d=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`

`d=sqrt((8-4)^2+((-10)-8)^2)`

`d=sqrt(340)=2sqrt(85)`

If diameter is `2sqrt(85)` then the radius is `(2sqrt(85))/2=sqrt(85)`

General equation of a circle is:

`(x-k)^2+(y-h)^2=r^2`

Where `k and h` are the `x and y` coordinates of the centre, and `r` is the radius:

Plugging in our values we found previously:

`k=6` , `h=-1` , `r=sqrt(85)`

`(x-6)^2+(y+1)^2=85`

This is the equation of the circle.

Graph: