What's the range and domain of f(x)=1/(root(x^2+3))? and how to prove it's not one to one function?
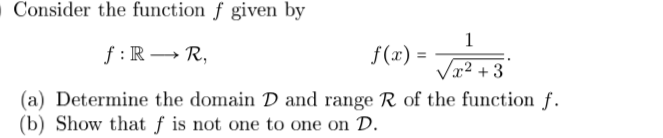
1 Answer
Apr 14, 2018
Please see the explanation below.
Explanation:
a) The domain of f:
The range of f:
b) If f: ℝ → ℝ , then f is a one to one function when f(a) = f(b) and
a = b, on the other hand when f(a) = f(b) but a ≠ b, then the function f is not one to one, so in this case:
f(-1) = f(1) = 1/2, but -1 ≠ 1, hence the function f is not one to one on its domain.

