Question

What`s the surface area formula for a rectangular pyramid?

Answer 1

`"SA"=lw+lsqrt(h^2+(w/2)^2)+wsqrt(h^2+(l/2)^2)`

Explanation:

The surface area will be the sum of the rectangular base and the `4` triangles, in which there are `2` pairs of congruent triangles.

Area of the Rectangular Base

The base simply has an area of `lw`, since it's a rectangle.

`=>lw`

Area of Front and Back Triangles

The area of a triangle is found through the formula `A=1/2("base")("height")`.

Here, the base is `l`. To find the height of the triangle, we must find the slant height on that side of the triangle.

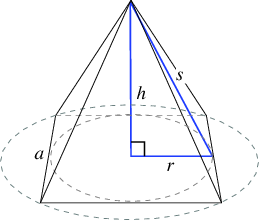
The slant height can be found through solving for the hypotenuse of a right triangle on the interior of the pyramid.

The two bases of the triangle will be the height of the pyramid, `h`, and one half the width, `w/2`. Through the Pythagorean theorem, we can see that the slant height is equal to `sqrt(h^2+(w/2)^2)`.

This is the height of the triangular face. Thus, the area of front triangle is `1/2lsqrt(h^2+(w/2)^2)`. Since the back triangle is congruent to the front, their combined area is twice the previous expression, or

`=>lsqrt(h^2+(w/2)^2)`

Area of the Side Triangles

The side triangles' area can be found in a way very similar to that of the front and back triangles, except for that their slant height is `sqrt(h^2+(l/2)^2)`. Thus, the area of one of the triangles is `1/2wsqrt(h^2+(l/2)^2)` and both the triangles combined is

`=>wsqrt(h^2+(l/2)^2)`

Total Surface Area

Simply add all of the areas of the faces.

`"SA"=lw+lsqrt(h^2+(w/2)^2)+wsqrt(h^2+(l/2)^2)`

This is not a formula you should ever attempt to memorize. Rather, this an exercise of truly understanding the geometry of the triangular prism (as well as a bit of algebra).