What volume (in mL's) of a 6.0 M stock solution of HCl should be used to prepare 6.00 L of a 0.250 M HCl solution?
1 Answer
Explanation:
Let's assume for a second that you're not familiar with the equation for dilution calculations.
What would your approach be here?
As you know, diluting a solution means keeping the number of moles of solute constant while increasing the total volume of the solution by adding more solvent.
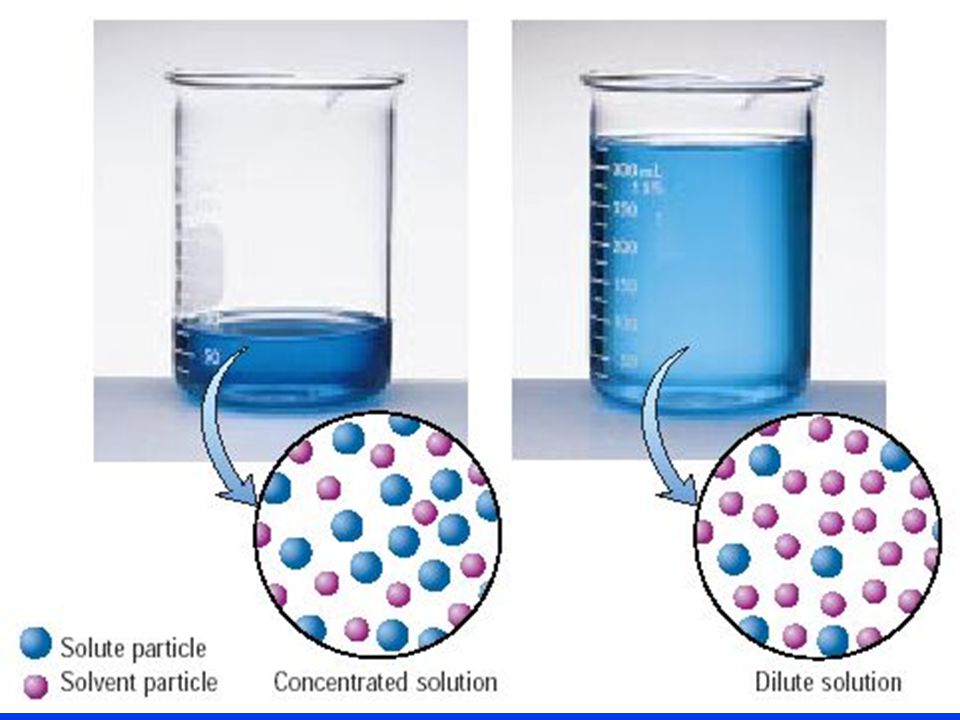
Since molarity is defined as moles of solute per liters of solution, diluting a solution will result in a decrease in its concentration.
So, if the number of moles of solute must be constant in order for a dilution to be performed, you can use the molarity and volume of the target solution to figure out how many moles of solute must be present in the sample of stock solution you're diluting.
#color(blue)(c = n/V implies n = c * V)#
#n_(HCl) = "0.250 M" * "6.00 L" = "1.5 moles HCl"#
Now all you have to do is figure out what volume of
#color(blue)(c = n/V implies V = n/c)#
#V_"stock" = (1.5 color(red)(cancel(color(black)("moles"))))/(6.0 color(red)(cancel(color(black)("moles")))/"L") = "0.25 L"#
Expressed in milliliters, the answer will be
#V_"stock" = color(green)("250 mL") -># rounded to two sig figs
This is the principle behind the equation for dilution calculations, which looks like this
#color(blue)(c_1V_1 = c_2V_2)" "# , where
Notice that you actually have
#overbrace(c_1V_1)^(stackrel( color(brown)("moles of solute"))(color(brown)("in stock solution"))) = overbrace(c_2V_2)^(stackrel(color(purple)("moles of solute"))(color(purple)("in target solution")))#
In your case, you'll once again get
#V_1 = c_2/c_1 * V_2#
#V_1 = (0.250 color(red)(cancel(color(black)("M"))))/(6.0color(red)(cancel(color(black)("M")))) * "6.00 L" = "0.25 L" = color(green)("250 L")#

