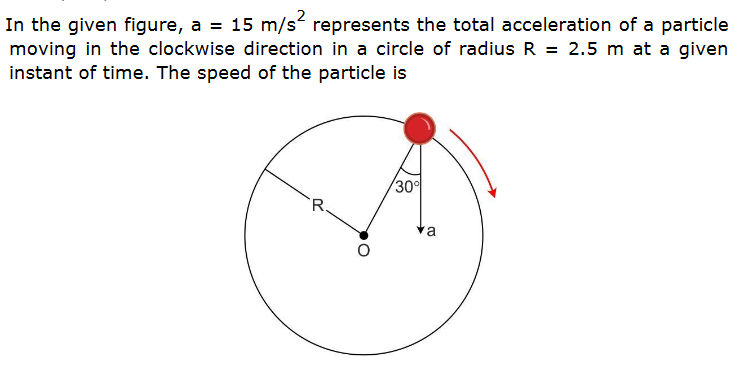
What will be the anser?
2 Answers
Explanation:
Here,considering speed to be the magnitude of linear velocity.
So,if it is moving with constant speed of
If its linear acceleration is
Given,
Again angle between
So,
Or,
Given,
If,
I.e
Given,
So, putting the values and arranging we get,
Putting this value of
Slightly shorter approach, same answer
Acceleration vector in non-uniform circular motion is:
#bba(t) = underbrace(r dot theta \ bbhat e_theta)_("tangential ") - underbrace(v^2/r\ bb hat e_r)_("inward radial: " = bba_r) #
In given geometry:


