What will be the ratio of the wavelength of the first line to that of the second line of paschen series of H atom? A)256:175 B)175:256 C)15:16 D)24:27
1 Answer
The answer is (A)
Explanation:
Your tool of choice here will be the Rydberg equation, which tells you the wavelength,
#1/(lamda) = R * (1/n_f^2 - 1/n_i^2)#
Here
#R# is the Rydberg constant, equal to#1.097 * 10^(7)# #"m"^(-1)# #n_i# is the initial energy level of the electron#n_f# is the final energy level of the electron
Now, the Paschen series is characterized by
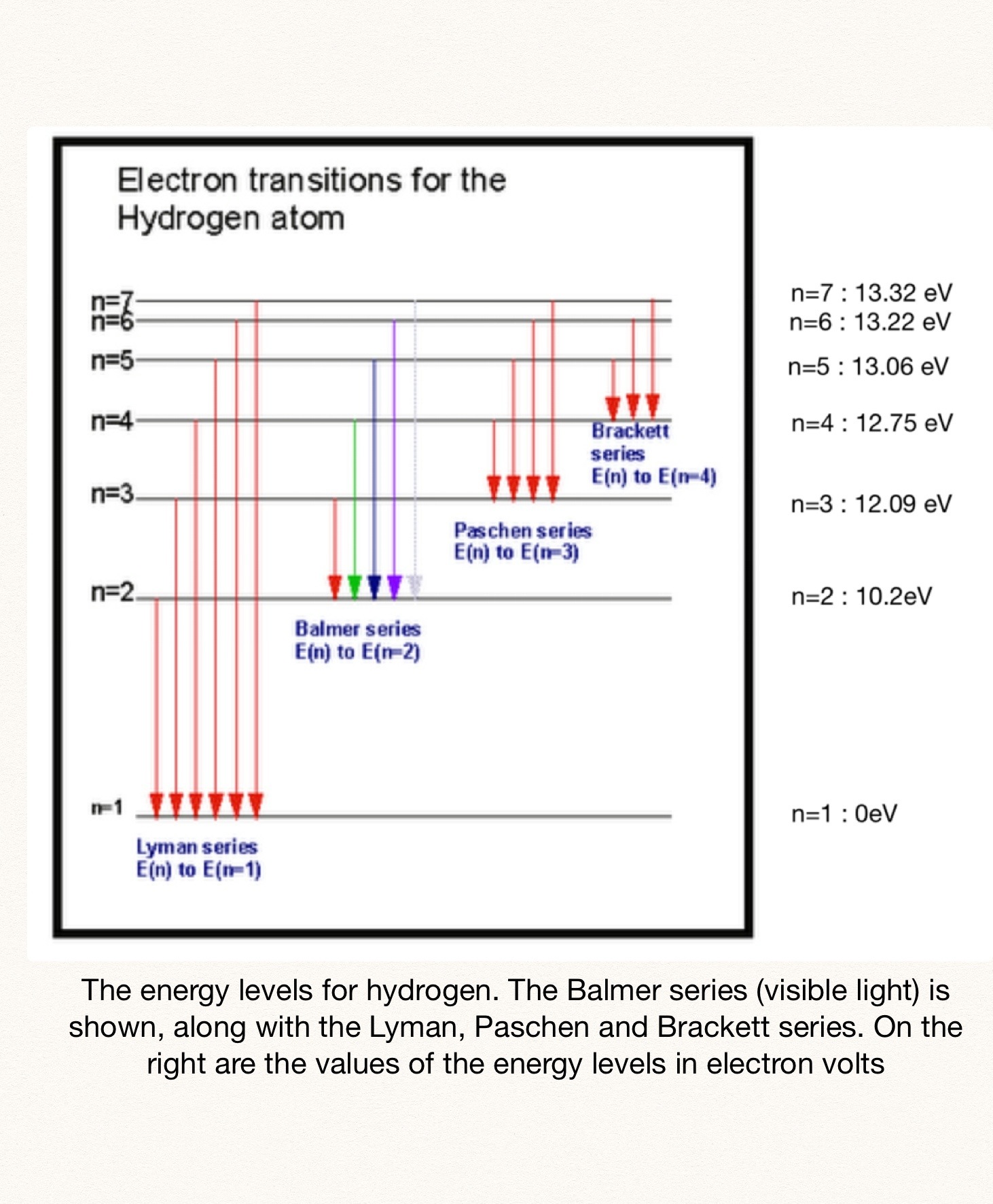
The first transition in the Paschen series corresponds to
#n_i = 4" " -> " " n_f = 3#
In this transition, the electron drops from the fourth energy level to the third energy level.
You will have
#1/(lamda_1) = R * (1/3^2 - 1/4^2)#
The second transition in the Paschen series corresponds to
#n_i = 5 " " -> " " n_f = 3#
This time, you have
#1/(lamda_2) = R * (1/3^2 - 1/5^2)#
Now, to get the ratio of the first line to that of the second line, you need to divide the second equation by the first one.
#(1/(lamda_2))/(1/(lamda_1)) = (color(red)(cancel(color(black)(R))) * (1/3^2 - 1/4^2))/(color(red)(cancel(color(black)(R))) * (1/3^2 - 1/5^2))#
This will be equivalent to
#(lamda_1)/(lamda_2) =(1/9 - 1/25)/ (1/9 - 1/16)#
#(lamda_1)/(lamda_2) = ((25 - 9)/(25 * 9))/((16 - 9)/(16 * 9)) = 16/(25 * color(red)(cancel(color(black)(9)))) * (16 * color(red)(cancel(color(black)(9))))/7 = 16^2/(25 * 7)#
Therefore, you can say that you have
#(lamda_1)/(lamda_2) = 256/175#

