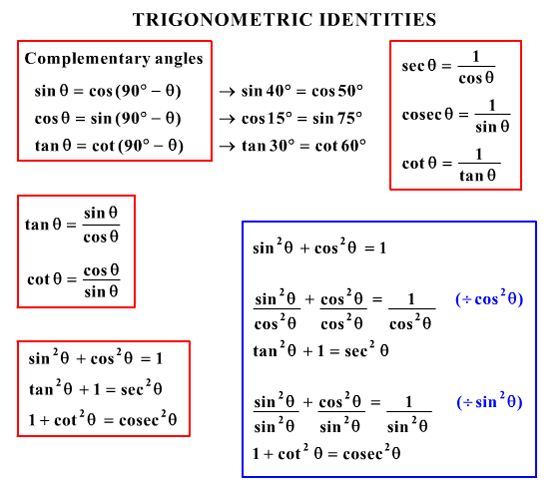
What would be steps in proving that [(tan2x)/(secx + 1)] + 1 = sec x ?
[(sec2x - 1)/(secx + 1)] + 1
[(secx - 1)(secx + 1)/(secx + 1)] + 1
(secx - 1) + 1
None of these
[(sec2x - 1)/(secx + 1)] + 1
[(secx - 1)(secx + 1)/(secx + 1)] + 1
(secx - 1) + 1
None of these
1 Answer
Apr 17, 2018
As proved.
Explanation: