When is a gas most likely to change to the liquid phase in terms of pressure?
1 Answer
When one reaches a particular pressure at a particular temperature where the phase equilibrium line is crossed on a phase diagram. Usually, this is when we increase the pressure at ordinary temperatures, but there are other scenarios not discussed, such as decreasing the temperature at ordinary pressures.
Consider a general phase diagram:
Looking at the blue curve, which is known as the liquid-vapor coexistence curve, when we cross that curve from left to right or top to bottom, we perform a liquid-vapor phase transition, i.e. either a condensation (
When we are just barely crossing the curve, infinitesimally slowly, we have that the chemical potential of the liquid phase is equal to that of the gas phase:
#mu_((l))(T^"*",P^"*") = mu_((g))(T^"*",P^"*")# where the chemical potential (a function of the temperature and pressure) is the molar Gibbs' free energy,
#mu(T,P) = barG(T,P) = (G(T,P))/n# , and is analogous to potential energy (it minimizes itself).
So, at the particular temperature
This is where the blue curve is crossed on the above diagram. Usually, this is when we increase the pressure at ordinary temperatures, but there are other scenarios not discussed, such as decreasing the temperature at ordinary pressures.
As a side note, the slope of the phase-phase coexistence curve is defined by the Clapeyron equation:
#(dP)/(dT) = (DeltabarH_(trs))/(T_(trs)DeltabarV_(trs))# ,where:
#DeltabarH_(trs)# is the change in molar enthalpy for the phase transition.#T_(trs)# is the phase transition temperature (i.e. boiling point, melting point, etc).#DeltabarV_(trs)# is the change in molar volume of the substance when going from one phase to another phase.
For example, the heat that goes into ice to melt it is given by
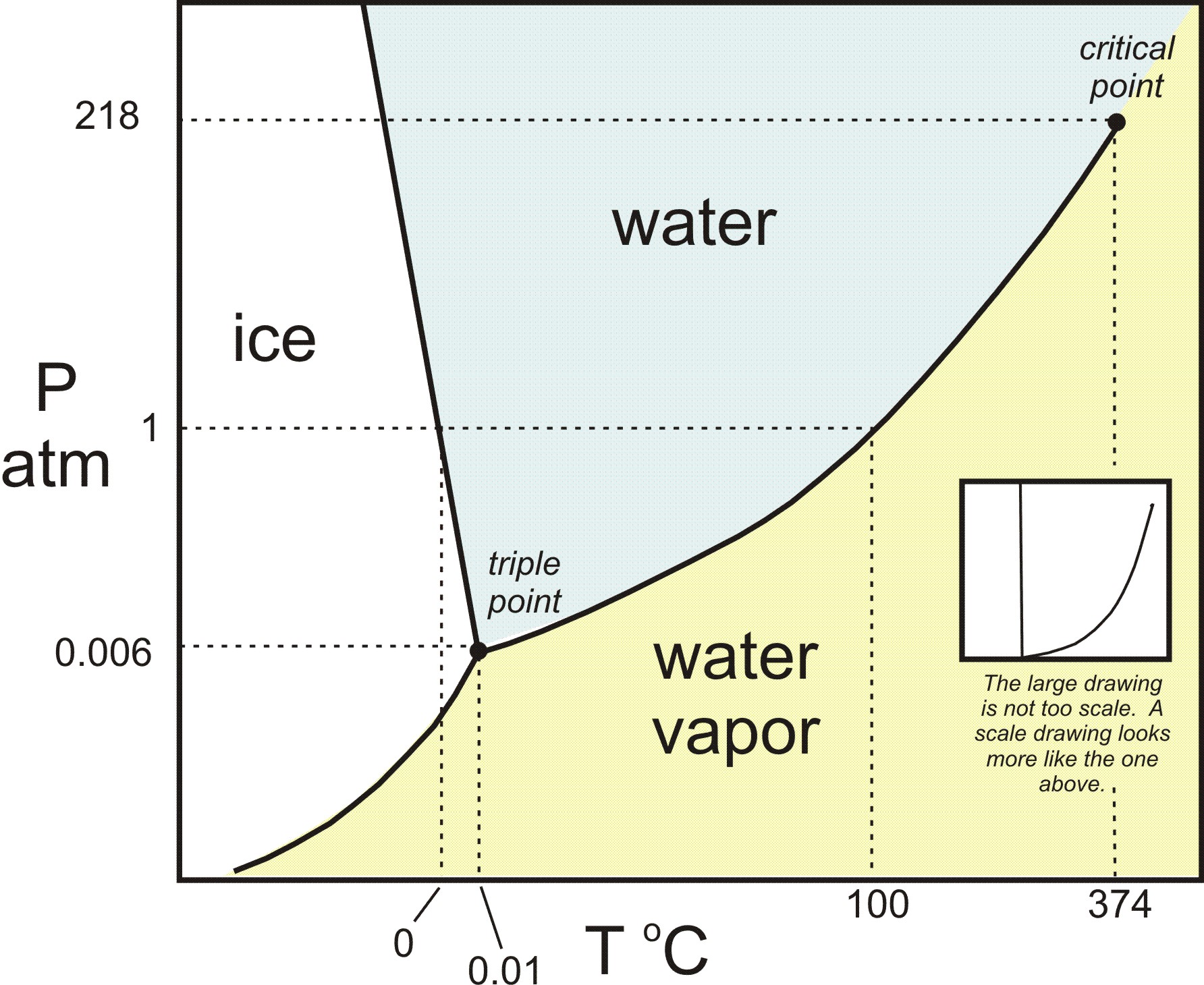
...the slope of the solid-liquid coexistence curve on water's phase diagram is negative. So, we get:
#stackrel((-))overbrace((dP)/(dT)) = (stackrel((+))overbrace(DeltabarH_(trs)))/(stackrel((+))overbrace(T_(trs))DeltabarV_(trs))#
Therefore, the change in molar volume of water when it melts must be negative. But the final state of melting is liquid water.
That means that the molar volume of liquid water is less than the molar volume of ice, i.e. ice contracts when it melts, or water expands when it freezes.

