Question

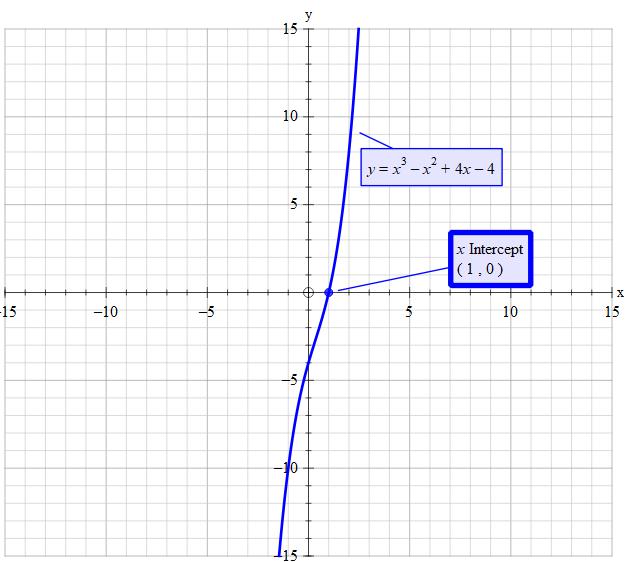
Which is a list of all the roots of `x^3 - x^2 = 4 - 4xcolor(white)(.)`? a. (-1,2,-2) ; b. (1,2,-2) ; c. (-1,2i,-2i) ; d. (1,2i,-2i)

Answer 1

d.

Explanation:

Substitute -1 for x:

`-1^3 - -1^2 != 4 - 4(-1)`

This eliminates selections a and c.

Substitute 2 for x:

`2^3 - 2^2 = 4 - 4(2)`

`8 - 4 = 4 - 8`

`4 != -4`

This eliminates selection b.

The remaining selection is d

Answer 2

The answer is d

Explanation:

Write as: `color(white)(d)x^3-x^2+4x-4=0`

`color(blue)("First stage - factoring groups:")`

`x^2(x-1)+4(x-1)=0`

Factoring out the `(x-1)`

`(x-1)(x^2+4)=0 larr" One if the factors is +1"`
...........................................................................
This is problematic as if we had `(x^2-2^2)` we could take it one step further.

I did investigate trying to force it so that we can have the structure:
`-(-x^2+2^2)=-(2^2-x^2)`

However, Although it yielded values matching b I found that substituting the values back into the original equation they failed.
..................................................................................
`color(blue)("Reworking of stage 2")`

Consider `(x^2+4)=0`

Using `y=ax^2+bx+c` where `a=1`; `b=0`; `c=4`

`x=(-b+-sqrt(b^2-4ac))/(2a) = (-0+-sqrt(0^2-4(1)(4)))/(2(1))`

`x=+-sqrt(-16/4) = +-2i`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
So the roots are `1; +2i; -2i`

Giving d as the solution