Question

Which is the correct answer?

A function, f, passes through the points (1,1), (2,7) and (3,25). A function, g, passes through the points (1,36), (2,43) and (3,50).

Select the correct answer.

As the value of x increases, the value of f(x) will never exceed the value of g(x).

As the value of x increases, the value of f(x) will eventually exceed the value of g(x).

As the value of x increases, the values of f(x) and g(x) remain constant.

As the value of x increases, the value of f(x) and the value of g(x) both approach 100.

Answer 1

I think it is likely that the intended answer was
"As the value of x increases, the value of f(x) will eventual exceed the value of g(x)"
however...

Explanation:

Without any information about the nature of `f(x)` and `g(x)` this question can not be definitively answered. 3 points are not enough to define a function (unless, for example,m we know that the function is a polynomial of degree 2 or less).

From the given information, it seems that `f(x)` is likely intended to increase by some non-linear factor, whereas `g(x)` is likely intended to be linear.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

If `f(x)` and `g(x)` are assumed to be continuous polynomial functions with minimal degrees to satisfy the given data,
then
`color(white)("XXX")f(x)=6x^2-12x+7`
and
`color(white)("XXX")g(x)=7x+29`
From the graphs we can see that in this case for large values of `x`, `f(x) > g(x)`

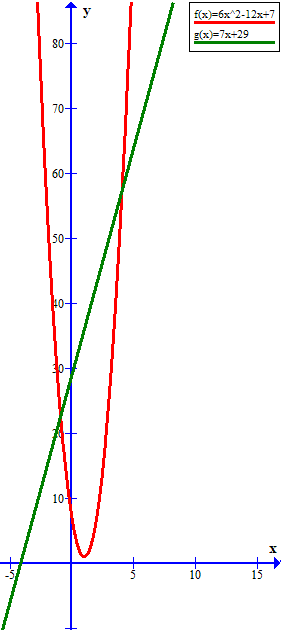
However (removing the requirement that `f(x)` have minimal degree)
`color(white)("XXX")f(x)=-6x^3+42x^2-78x+43`
also fits the given data values, but the graphs now look like:

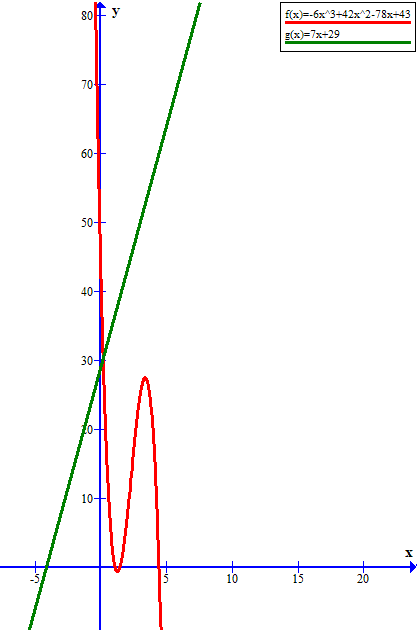
and except of small values of `x`, `f(x) < g(x)`

Similarly, if `g(x)` is not of minimal degree... and if we remove the assumption of continuity then anything is possible.