Which set of ordered pairs does not represent a function?
{(3, 7), (–1, 9), (–5, 11)}
{(9, –5), (4, –5), (–1, 7)}
{(–2, 1), (3, –4), (–2, –6)}
{(3, 7), (–1, 9), (–5, 11)}
{(9, –5), (4, –5), (–1, 7)}
{(–2, 1), (3, –4), (–2, –6)}
2 Answers
The last one
Explanation:
A function has to return a unique value when given an argument. In the last set
Additional technical points
There is another important part of the definition of a function that we should really worry about here. A function is defined with a domain - the set of input values that it takes, as well as a codomain - the set of possible values it can return (some books call this range).
A function has to return a value for each element of the domain. Since the domain has not been specified for any of the prospective functions here, we can not be sure that even the other two fit the criteria to be a function.
What we can say is :
-
{(3, 7), (–1, 9), (–5, 11)} can represent a function if the domain is specified as the set{3,-1,-5} -
{(9, –5), (4, –5), (–1, 7)} can represent a function if the domain is specified as the set{9,4,-1}
In both cases the codomain can be taken to be the set of integers (it is not demanded of a function that it returns every value in the codomain - just that every value it does return is in the codomain)
Explanation:
Given: Three Sets of Relations, say
Definition of a Relation:
A relation is simply a set of input and output values, represented in ordered pairs.
Any set of ordered pairs may be used in a relation.
No special rules are available to form a relation.
Definition of a Function:
A function is a set of ordered pairs in which each x-element has Only One y-element associated with it.
Examine the three sets of relations given to determine if any of them strictly follows the rule for being a function.
Set the Input data table up:
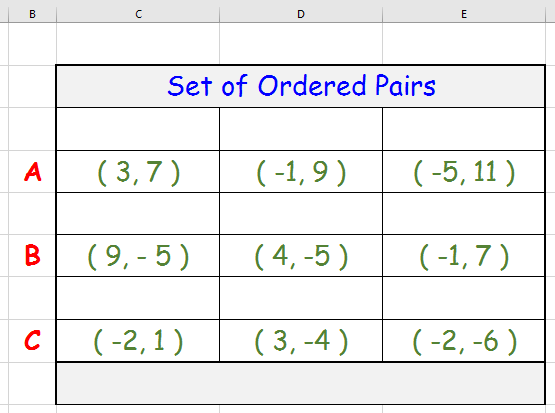
Rewrite the data table to facilitate comparing
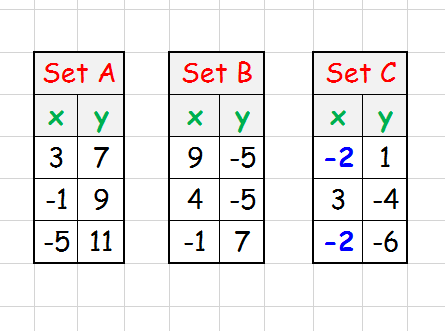
A simple visual examination tells us that
Note that
But, x-coordinate values are NOT repeated.
Set B is a function using the rule.
Hence,
Plot ordered pairs of
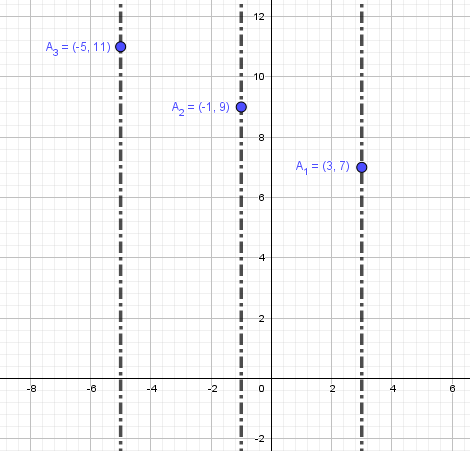
Plot ordered pairs of
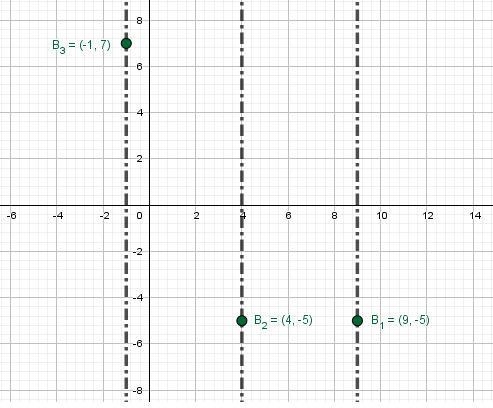
Plot ordered pairs of
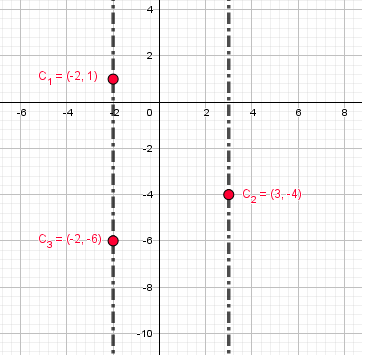
Hope it helps.


