Because they cannot ever touch those zones, and they never will.
Refer to this function:
#f(x)=1/x#
It should look something like this:
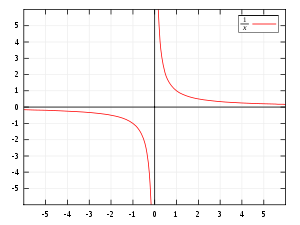
You can see where the horizontal asymptote and the vertical asymptote exist.
So what is an asymptote exactly?
A rational function cannot touch the asymptote, but why?
What happens if you make #x=0# in the function? In a calculator, you may get a divide by 0 error, that is what happens when you touch a vertical asymptote, bad things happen. Your best bet is to make #x# a ridiculously small number to get an absurdly large answer.
Similarly, making #x# an absurdly large number would probably result as a 0 on some calculators, but the actual result is, of course, a ridiculously small number. The only way that function can EVER touch the horizontal asymptote is if #x=oo#, but that can never happen. Infinity is just continuously going up into big numbers with no end. Calculators may say "Overflow error" from this because computers can't compute numbers that large.
Basically, asymptotes are hypothetical positions a function may approach, but will never touch.


