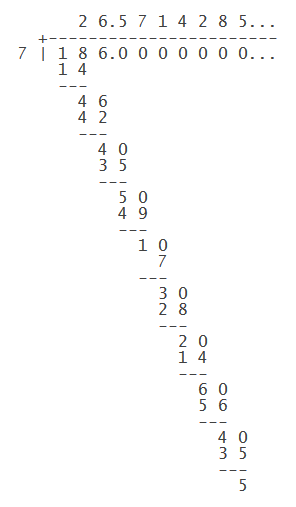Suppose #p/q# is a rational number, where #p# and #q# are both integers and #q > 0#.
To obtain the decimal expansion of #p/q# you can long divide #p# by #q#.
During the process of long division, you eventually run out of digits to bring down from the dividend #p#. From that point on, the digits of the quotient are determined purely by the sequence of values of the running remainder, which is always in the range #0# to #q-1#.
Since there only #q# different possible values for the running remainder, it will eventually repeat, and so will the digits of the quotient from that point.
For example: #186/7# ...
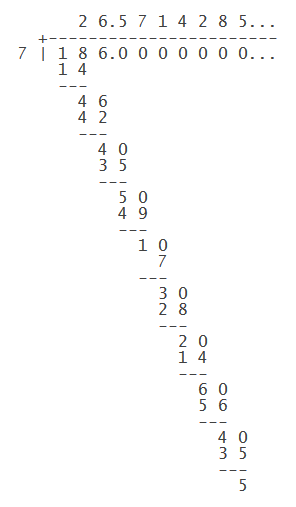
Notice the sequence of remainders: #4, color(blue)(4), 5, 1, 3, 2, 6, color(blue)(4), 5# which starts to repeat again.