Question

Why do the midpoints of a rhombus form a rectangle? Solved in a paragraph proof.

Answer 1

see explanation.

Explanation:

Some of the properties of a rhombus :
1) all sides are congruent, `=> AB=BC=CD=DA`,
2) opposite angles are congruent, `=> angleADC=angleABC=y`,
and `angleBAD=angleBCD=x`,
3) adjacent angles are supplementary, `=> x+y=180^@`
4) opposite sides are parallel, `=> AD` // `BC, and AB` // `DC`,

given that `P,Q, R and S` are midpoints of `AB,BC,CD, and DA`, respectively,
`=> AP=PB=BQ=QC=CR=RD=DS=SA`
Consider `DeltaAPS`, as `AP=AS, => DeltaAPS` is isosceles,
`=> angleASP=angleAPS=w`,
`=> x+2w=180^@ ----- Eq(1)`
Consider `DeltaBPQ`, as `BP=BQ, => DeltaBPQ` is isosceles,
`=> angleBPQ=angleBQS=z`
`=> y+2z=180^@ ----- Eq(2)`
`Eq(1)+Eq(2) = (x+y)+2(w+z)=360^@`
`=> 180+2(w+z)=360^@`
`=> w+z=90^@`
`=> angleSPQ=180-(w+z)=180-90=90^@`
Similarly, `anglePQR=angleQRS=angleRSP=180-(w+z)=90^@`

Hence, `PQRS` is a rectangle.

Answer 2

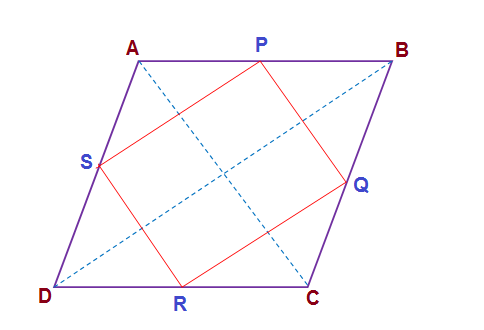
Given
In the above figure `ABCD` is a rhombus where sides `AB=BC=CD=DA`.
`P,Q,R,S` are the midpoints of sides `AB,BC,CD,DA` respectively,

`P,Q,R,S` are joined in order to form the quadrilateral `PQRS` .

Rtp
We are to prove `PQRS` is always rectangle.

Construction
Diagonals `AC and BD` of the rhombus are drawn.
Proof
Now by midpoint theorem of a triangle any two opposite sides of the rectangle `PQRS` are parallel and half of the diagonal.

So `PQ=SR=1/2AC and PQ||AC, SR||AC`
Hence in `PQRS,` `PQ=SR and PQ||SR`. Hence `PQRS` is a parallelogram.

So `PS=RQ and PS||RQ||BD`
And `PQ=SR and PQ||SR||AC`

But `AC_|_BD` as these are diagonals of a rhombus.
Hence adjacent sides of the quadrilateral,which are parallel to diagonals, must be perpendicular to each other, This proves that `PQRS` is a rectangle.