Why does the equation 4x^2-25y^2-24x-50y+11=0 not take the form of a hyperbola, despite the fact that the squared terms of the equation have different signs? Also, why can this equation be put in the form of hyperbola(2(x-3)^2)/13 - (2(y+1)^2)/26=1
3 Answers
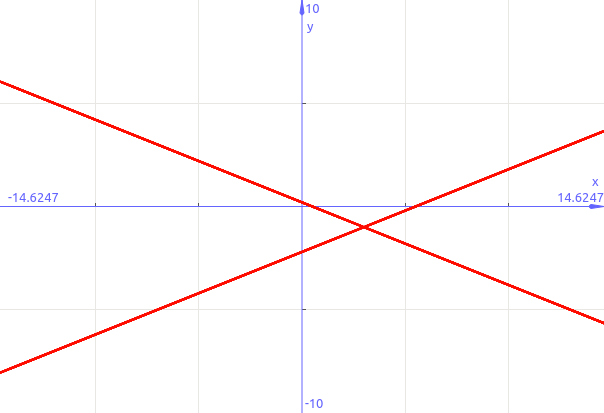
To people, answering the question, please note this graph: https://www.desmos.com/calculator/jixsqaffyw
Also, here is the work for getting the equation into the form of a hyperbola: 
Actually, this is not what I have:
I have that
so it's a reducible conic whose polynomial has real roots
So it splits up in 2 real-valued lines which intersecate in the center
The first statement is only necessary to have an hyperbola: you need also the equation not to be reducible, or you have a degenerate conic.
Check your calculations, and don't worry, everybody makes mistakes in calculations :)
The graph of the equation