Why is AM=MB=MC in this right triangle?

Question

I understand that AM=BC because M is the centerpoint, but I do not understand MC.

1547 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-07-20T10:52:00

Please refer to the Explanation.

#M# is the midpoint of #AB# and #/_ACB=90^@#.

Therefore, #C# lies on the (semi)circle described on #AB,# taking #AB#

as diameter.

#M# is the midpoint of the diameter #AB#.

#:. M# is the centre of the circle.

Thus, #C# lies on the circle having centre at #M# and a diameter #AB#.

Clearly, #MA=MB=MC"(=the radius of the circle)"#.

Answer 2 · 2018-07-20T11:41:11

Please see below.

Your Question :
I understand that #AM=color(red)(BC)# because #M# is

the centerpoint, but I do not understand #MC.#

I think it is #AM=MB and# not #color(red)(BC)#

We have two Theorem :

#color(green)((1) "An angle inscribed in a semicircle is a right angle"#

#color(green)((2)"The circle whose diameter is the hypotenuse of the "#

#color(green)("right triangle , passes through three vertices of the triangle."#

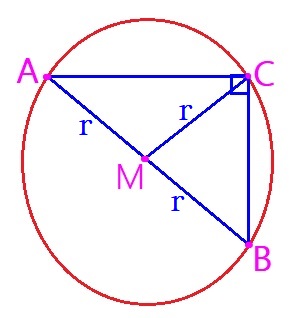
enter image source here

So, #A ,B, and C# are the points on the circle and #mangleC=90^circ#

#:.color(violet)( " Hypotenuse AB of triangle = Diameter AB of circle"#

Now , #M " is the midpoint of AB"#

So, #"M is the center of the circle. "#

Let #color(blue)(r)# be the radius of circle.

#:.color(blue)(AM= MB=r#

Here, #bar(MC)# is the line segment joining center #M # and vertex #C#

#:. MC " is the radius of circle."#

#:.color(blue)( MC =r)#

Hence ,

#color(blue)(AM=MB=MC=r#