Question

Why is the [specific] heat capacity of water high?

Answer 1

Most likely due to its hydrogen-bonding.

These intermolecular forces are particularly strong, and are distance- and angle-dependent.

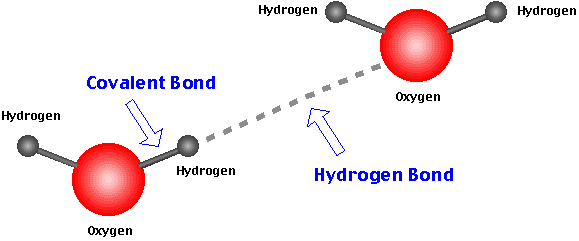
They strongly hold together the water molecules together and make them liquid phase at room temperature and pressure. This is also why water has a high boiling point.

That allows water molecules to absorb a lot of heat before vibrating all that much, which leads to a high specific heat capacity.

---

For comparison, consider the specific heat capacities (typically at constant pressure) below, from NIST unless otherwise specified:

`"H"_2"O": C_P = "4.1841 J/g"^@ "C"` at `"298 K"`

`"H"_2"S": C_P = "1.0050 J/g"^@ "C"` at `"298 K"`

`"H"_2"Se": C_P = "0.4285 J/g"^@ "C"` at `"298 K"`

And we do indeed see a significantly higher specific heat capacity for water than for compounds analogous to water.

The specific heat capacity from a statistical mechanics point of view is basically the capacity to store energy in certain energy levels (translational, rotational, vibrational, electronic).

When these energy levels are low, the minimum temperatures required to occupy those energy levels are also low, so they are easily occupied.

Ignoring electronic energy levels, which tend to not be occupied at SATP, for these molecules, we have the following rotational and vibrational temperatures, `Theta_(rot)` and `Theta_(vib)`:

`color(white)([("",color(black)("H"_2"O"),color(black)("H"_2"S"),color(black)("H"_2"Se")),(color(black)(color(black)(Theta_(rot) ("K"))),(color(black)(40.11, 20.88, 13.36)),(color(black)(14.89, 13.00, 6.80)),(color(black)(11.72, 11.16, 5.61))),(color(black)(Theta_(vib) ("K")),(color(red)(5262, 2295, 5404)),(color(green)(3763, 1702, 3778)),(color(green)(3374, 1488, 3393)))])`

With low `Theta_(rot)` values, this means that at ordinary temperatures, all three of these molecules are easily rotating.

However, if you notice, the vibrational temperatures `Theta_(vib)` are significantly higher for water than for `"H"_2"S"` and `"H"_2"Se"` (about `"500 - 2000 K"` higher in this case).

That means water can take in a lot of heat before it vibrates to a significant extent (occupies its vibrational states), and that gives rise to a high specific heat capacity.

This is likely a result of its hydrogen-bonding, which try to fix the protons in place for the interaction, which is both distance- and angle-dependent. That would make it difficult to get water to stretch and bend its bonds in bulk solution.