Question

Why is the rate determining step slow?

Answer 1

I think you meant, "why is a slow step rate-determining?", and I think it's more productive to answer that instead.

Rate-determining steps are slow because of how the mechanism works, which is just another way of saying "it is what it is", and isn't much of an answer.

---

WHAT DOES IT MEAN IF A MECHANISTIC STEP IS "SLOW"?

It's not rocket science; it's kinetics, and when we think "kinetics", we should think about time.

A step in a reaction mechanism is (kinetically) slow when it literally takes the longest time out of all the steps to occur.

Another way to define it is...

The rate of a mechanistic step is considered slow when it is most similar to the rate of the overall reaction.

A simple way to think about this is considering how averages work.

1. Large numbers contribute more to an average than small numbers.
2. Large times are slow times.

So, we say that on average, a slow step (a small `r(t)`) basically determines the rate of reaction---it is the rate-determining step. That's pretty much it.

The slower the "slow step", the slower the rate of the overall reaction (the smaller `r(t)` is).

WHAT MIGHT MAKE THIS STEP SO SLOW?

Basically, whatever would make it hard for the reactants to collide effectively. Steric hindrance (bulky molecules) is a common reason, amongst others.

So, for an `"S"_N1` reaction with a tertiary alkyl halide...

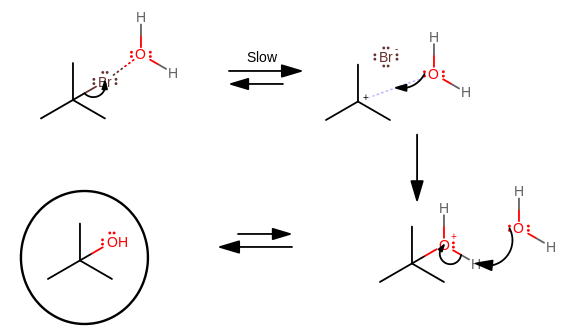
...the slow step is the one where we wait for the halide to fall off to form the carbocation; the nucleophile isn't strong (fast) enough to overcome the bulkiness (a kinetic barrier) of the tertiary alkyl halide.

EXAMPLE

Let's say we had an overall reaction like this:

`O_3(g) + O(g) -> 2O_2(g)`

where:

• `->` (an overall reaction) indicates that the reaction as-written has more to it than what you see here.
• `=>` (an elementary step) indicates that there is NOT more to it than what you see here.

The accepted mechanism for bimolecular ozone destruction in my book, catalyzed by `Cl(g)` and forming the `ClO(g)` intermediate, is:

`O_3(g) + cancel(Cl(g)) stackrel(k_1; "assumed slow"" ")(=>) cancel(ClO(g)) + O_2(g)`
`cancel(ClO(g)) + O(g) stackrel(k_2" ")(=>) O_2(g) + cancel(Cl(g))`
`"------------------------------------------"`
`O_3(g) + O(g) stackrel(k_"obs"" ")(->) 2O_2(g)`

...which you see cancels out to give the same overall reaction.

Now, to emphasize, I am arbitrarily picking out a hypothetical slow step. I'm not actually sure which step is the slow step.

The point is, we have the rate laws as:

`r(t) = k_"obs"["O"_3]["O"]`
`r_1(t) = k_1["O"_3]["Cl"]`
`r_2(t) = k_2["ClO"]["O"]`

• If step 1 was slow, then `|r_1(t) - r(t)| < |r_2(t) - r(t)|`, and `r_1(t) < r_2(t)`.
• If step 2 was slow, then `|r_1(t) - r(t)| > |r_2(t) - r(t)|`, and `r_2(t) < r_1(t)`.