Why is the second ionization energy greater than the first ionization energy in atoms?
1 Answer
Explanation:
Let's look at the process purely on the basis of electrostatics. It should take more energy to remove an electron from a positively charged atom, than from a neutral atom, because the valence electrons of a positive species should be more strongly attracted to the nuclear core, and shielding of the nuclear charge by electrons should diminish.
On this basis alone,
In the special case of the alkali metals, the second ionization energy would involve the removal of a non-valence, inner shell electron. And thus, in this instance,
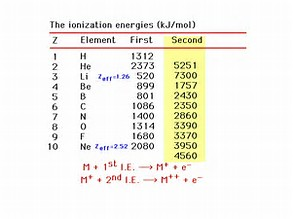
Are the given data consistent with what we have argued? Why is a second ionization energy not listed for hydrogen?

