Why is the spectrum of helium different from that of hydrogen?
1 Answer
Well, is it not just a different atom, with more than one electron? The spectrum of helium must be more complex, because now angular momentum becomes a factor to which transitions are allowed; it must change by
Examples:
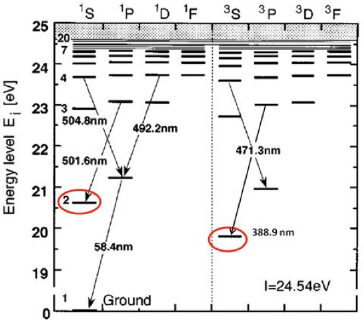
1s -> 2p ("58.4 nm" )
2s -> 3p ("501.6 nm" )
2p -> 4d ("492.2 nm" )
2p -> 4s ("504.8 nm" )
The energy levels of the hydrogen atom are well-known:
E_n = -"13.6058 eV" cdot Z^2/n^2 where
Z = 1 for hydrogen atom.
Those for helium have no straightforward formula, but are known experimentally.
Using Excel, and the energy levels of helium given numerically here (estimating the
These energy level gaps are different, and since transitions between them lead to a spectrum, the spectrum is of course also different...
To be fair, I ignored the
That occurs because having two electrons in helium introduces electron correlation, which splits levels of different angular momentum, because they no longer have spherical symmetry.
Beyond that difference, which is readily seen in multi-electron atoms having, e.g. orbital potential energies
- The lowest energy levels become lower for heavier atoms, knowing that the energy levels depend directly on atomic number squared.
- The lowest energy levels become more spread out from the rest, in larger atoms, obviously because bigger atoms have a greater effective nuclear charge
Z_(eff) , which is most easily seen via the most significant attraction of the core energy levels (n = 1 in both atoms).
Because the energy level gaps widen, we expect to see shifts in electronic transitions towards lower wavelength for helium compared to hydrogen.
(Indeed, the

