Why is there a discrepancy in the force constants of #"HBr"# vs. #"HCl"#?
We know that:
#tildeomega_0 = tildeomega_e - 2tildeomega_e chi_e#
where #tildeomega_0# is the forbidden frequency that is in the middle of the gap for #upsilon = 0 -> 1# in the infrared spectrum, #tildeomega_e# is the equilibrium fundamental frequency, and #tildeomega_e chi_e# is the anharmonicity constant.
NIST states:
#tildeomega_e ("HBr") = "2648.97 cm"^(-1)#
#tildeomega_e chi_e("HBr") = "45.2175 cm"^(-1)#
#tildeomega_e ("HCl") = "2990.95 cm"^(-1)#
#tildeomega_e chi_e("HCl") = "52.8186 cm"^(-1)#
Therefore, I get #tildeomega_0 = "2558.5 cm"^(-1)# for #"HBr"# and #"2885.3 cm"^(-1)# for #"HCl"# .
From a casual google search, I find that the force constant is given as #k = color(green)"410 N/m"# for #"HBr"# and #k = color(purple)"480 N/m"# for #"HCl"# . Here's the problem...
#k = mu omega^2#
where #mu = (m_1m_2)/(m_1 + m_2) cdot ("1 kg")/"1000 g" cdot "1 mol"/(6.0221413 xx 10^(23) "kg"# is the reduced mass (with #m_i# in #"g/mol"# ), and #omega# is the angular frequency in #"rad/s"# . My concern?
Is it #tildeomega_e = omega/(2pic)# , or #tildeomega_0 = omega/(2pic)# ?
#k("HBr") = mu(2pic tildeomega_e)^2#
#= 0.9951 cdot 1/1000 cdot 1/(6.0221413 xx 10^(23)) "kg" xx (2pi cdot 2.998 xx 10^(10) "cm/s" cdot "2648.97 cm"^(-1))^2#
#=# #color(green)"411.4 N/m"# , in agreement with HyperPhysics. But my gut says this is not right!
#k("HCl") = mu(2pic tildeomega_e)^2#
#= 0.9796 cdot 1/1000 cdot 1/(6.0221413 xx 10^(23)) "kg" xx (2pi cdot 2.998 xx 10^(10) "cm/s" cdot "2990.95 cm"^(-1))^2#
#=# #color(red)"516.3 N/m"# , not in agreement with HyperPhysics.
However, if I use #tildeomega_0# ...
#k("HCl") stackrel(?" ")(=) mu(2pic tildeomega_0)^2#
#= 0.9796 cdot 1/1000 cdot 1/(6.0221413 xx 10^(23)) "kg" xx (2pi cdot 2.998 xx 10^(10) "cm/s" cdot "2885.3 cm"^(-1))^2#
#=# #color(purple)"480.5 N/m"# , easily in agreement with HyperPhysics. But this I think is actually correct.
But I just used two different definitions of #omega# to get there. Contradiction much?
We know that:
where
#tildeomega_0# is the forbidden frequency that is in the middle of the gap for#upsilon = 0 -> 1# in the infrared spectrum,#tildeomega_e# is the equilibrium fundamental frequency, and#tildeomega_e chi_e# is the anharmonicity constant.
NIST states:
Therefore, I get
From a casual google search, I find that the force constant is given as
#k = mu omega^2#
where
Is it
#k("HBr") = mu(2pic tildeomega_e)^2#
#= 0.9951 cdot 1/1000 cdot 1/(6.0221413 xx 10^(23)) "kg" xx (2pi cdot 2.998 xx 10^(10) "cm/s" cdot "2648.97 cm"^(-1))^2#
#=# #color(green)"411.4 N/m"# , in agreement with HyperPhysics. But my gut says this is not right!
#k("HCl") = mu(2pic tildeomega_e)^2#
#= 0.9796 cdot 1/1000 cdot 1/(6.0221413 xx 10^(23)) "kg" xx (2pi cdot 2.998 xx 10^(10) "cm/s" cdot "2990.95 cm"^(-1))^2#
#=# #color(red)"516.3 N/m"# , not in agreement with HyperPhysics.
However, if I use
#k("HCl") stackrel(?" ")(=) mu(2pic tildeomega_0)^2#
#= 0.9796 cdot 1/1000 cdot 1/(6.0221413 xx 10^(23)) "kg" xx (2pi cdot 2.998 xx 10^(10) "cm/s" cdot "2885.3 cm"^(-1))^2#
#=# #color(purple)"480.5 N/m"# , easily in agreement with HyperPhysics. But this I think is actually correct.
But I just used two different definitions of
1 Answer
After some experimentation, what it looks like to me is that
#tildeomega_0 = omega/(2pic)# .
HyperPhysics seems to give
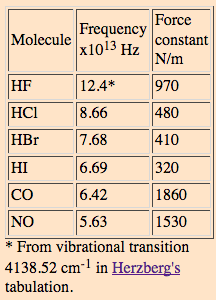
From NIST for

#tildeomega_e = "2648.975 cm"^(-1)#
#tildeomega_e chi_e = "45.2175 cm"^(-1)#
so as we said,
#tildeomega_0 = tildeomega_e - 2tildeomega_e chi_e#
#= 2648.975 - 2 cdot 45.2175# #"cm"^(-1) = "2558.2 cm"^(-1)#
If we say that
#nu = tildeomega_0 cdot c#
#= ("2558.2 cm"^(-1))(2.998 xx 10^10 "cm/s") #
#= ul(7.67 xx 10^(13) "s"^(-1))#
And on HyperPhysics, their table has a frequency listed of
(Had we assumed
So now we're in agreement that we're looking at
#omega = 2pi nu#
#= 2pi# #"rad/rev"cdot 7.68 xx 10^13 "s"^(-1)#
#= 4.83 xx 10^14 "rad/s"#
Then for the force constant, I get:
#color(blue)(k("HBr")) = mu omega^2#
#= overbrace([(1.007825*78.9183371)/(1.007825 + 78.9183371) "g"/"mol" cdot "1 kg"/"1000 g" cdot ("1 mol")/(6.0221413 xx 10^23)])^(mu) cdot (4.83 xx 10^14 "rad/s")^2#
#=# #color(blue)("385 N/m")# and not
#color(red)"411 N/m"# .
That seems to do it. Upon checking the rest of them, the following force constants are incorrect:
#"HBr"# - Should be#"385 N/m"# , not#"410 N/m"# .#"HI"# - Should be#"293 N/m"# , not#"320 N/m"# .
These look good:
#"HF"# - I got#"966 N/m"# compared to#"970 N/m"# .#"HCl"# - I see#"481 N/m"# compared to#"480 N/m"# .#"CO"# - I got#"1857 N/m"# compared to#"1860 N/m"# .#"NO"# - I got#"1551 N/m"# compared to#"1530 N/m"# .
So it's just

