Question

Why parametric equations of the parabola `y^2 = 4ax` is `y =2at` and `x = at^2` . why can't `y =4at` and `x = 4at^2`. Because `y = 4at` and `x = 4at^2` also satisfies the equation `y^2 = 4ax` right ?

Answer 1

Parametric equations are not unique.

Explanation:

Start with `y^2 = 4ax`

y is the domain and it is `-oo < y < oo`

x is the range and it is `0 <=x < oo`

Let's check your parametric equations `y = 4at` and `x = 4at^2`.

`(4at)^2 = 4a(4at^2)`

`16a^2t^2 = 16a^2t^2` It seems to satisfy the equation

y has the domain `-oo < y < oo`
x has the range `0 <= x < oo`

Let `a=2` and look at the two graphs for `color(red)(y^2 = 8x)` and `color(blue)((8t^2,8t); -oo < t < oo)`

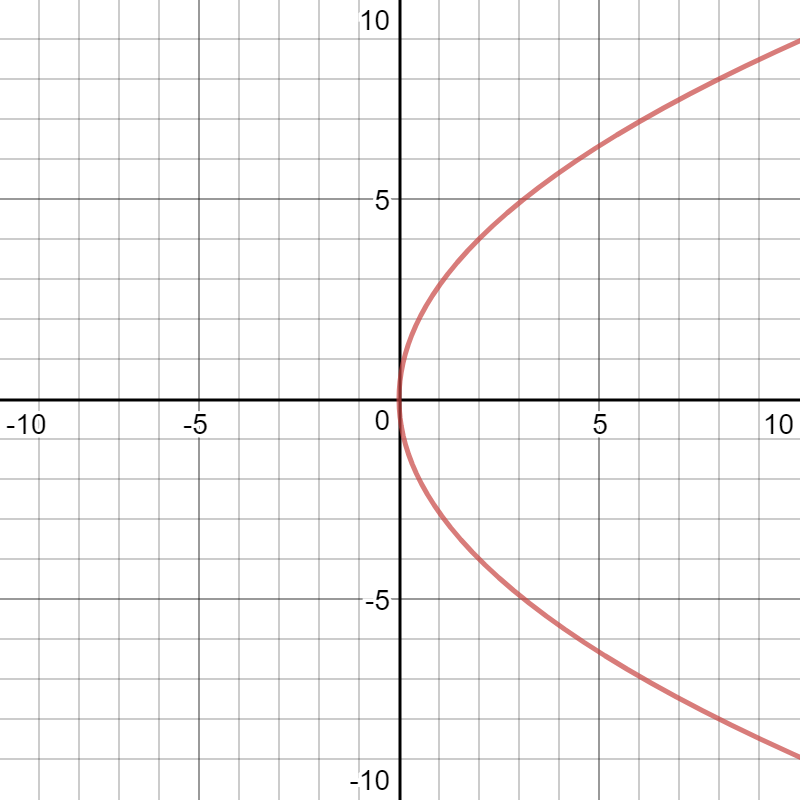
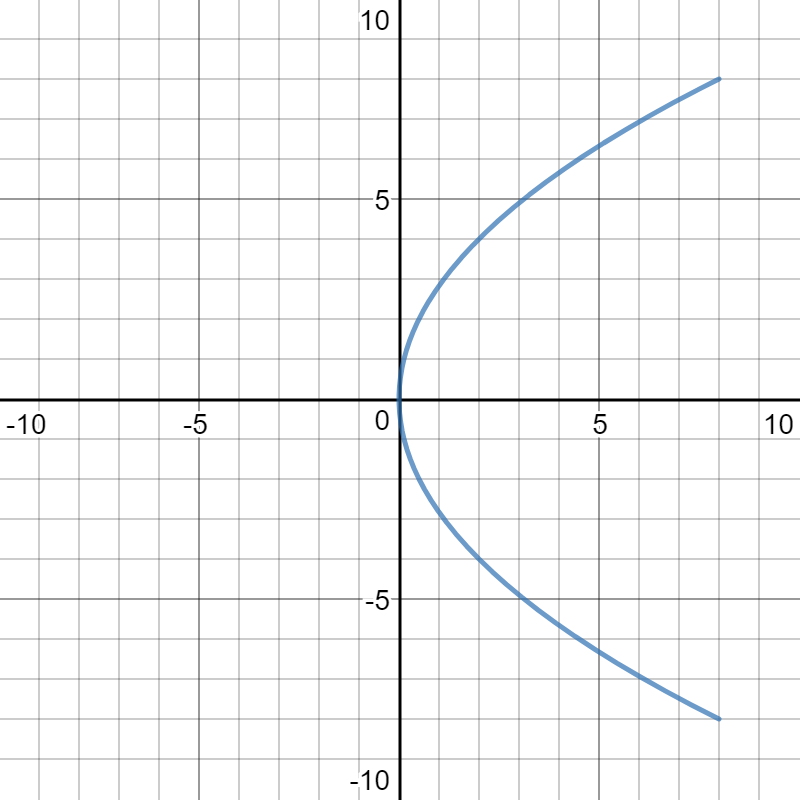
The two graphs are identical.

I am sure that you can find other parametric equations for the same graph. For example, `y = t` and `x = t^2/(4a)`