Would the image of an object be the same if we put it in front of a convex mirror, and in front of a diverging lens if they have the same focal length? If not, what would be the differences? (Distance of the object is the same in both conditions.)
1 Answer
In both cases the image is erect, virtual, diminished. Only difference is that in case convex mirror the image is formed behind it whereas in case of diverging lens the image is formed on the same side of the lens as the object is.
Explanation:
For an object to be placed in front of a convex mirror there are six distinct positions. These are the respective images produced are detailed below:
Let F be Focal Point, C its Center of Curvature where C=2F
-
Object is placed between F and the mirror
-
Object is placed at the Focal Point
-
Object is placed between F and C
-
Object at C
-
Object beyond center of curvature
-
Object at infinity
Ray diagram can be drawn for all locations of the object by observing the following rules*:
- Any ray parallel to the principal axis, will be reflected as if coming form the focus F.
- A ray which appears to pass through focus F, will be reflected and become parallel to the principal axis.
- A ray which appears to pass through C, will be reflected and appear as if coming from C.
As shown in the picture, ray diagram for a particular location all three rays of light starting from the top of the object need to be extended behind the mirror to find the position of the tip of image.
Image in all six instances is erect, virtual, diminished, behind the mirror and between mirror and F. Only for the sixth location it is situated at F and highly diminished to the size of a point.
We can also use the Mirror equation
Sign convention is that
Now we take the case of object placed in front of a diverging lens, that is a concave lens.
The ray diagram is as shown in the picture below for one of the six locations of the object.
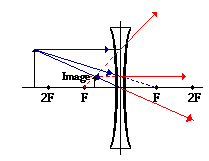
Ray diagram can be drawn for all locations of the object by observing the following rules*:
- Any ray parallel to the principal axis, will be refracted as if coming form the focus F of the same side of the object.
- A ray which appears to pass through focus F, will be refracted and become parallel to the principal axis.
- A ray which appears to pass through center of the lens, will be pass through the lens not refracted.
*Actually only any two out of these three are sufficient to obtain the position of the image.
To obtain the image the rays need to be extended back a shown. Image in all six instances is erect, virtual, diminished, on the same side of the lens as the object is and between lens and F. Only for the sixth location it is situated at F and highly diminished to the size of a point.
We can also use the Lens equation for diverging lens
And Linear magnification
Given that focal length is same for both convex mirror, diverging lens, therefore we obtain same result.
Except that in case mirror the image is formed behind it whereas in case of diverging lens the image is formed on the same side of the lens as the object is.
