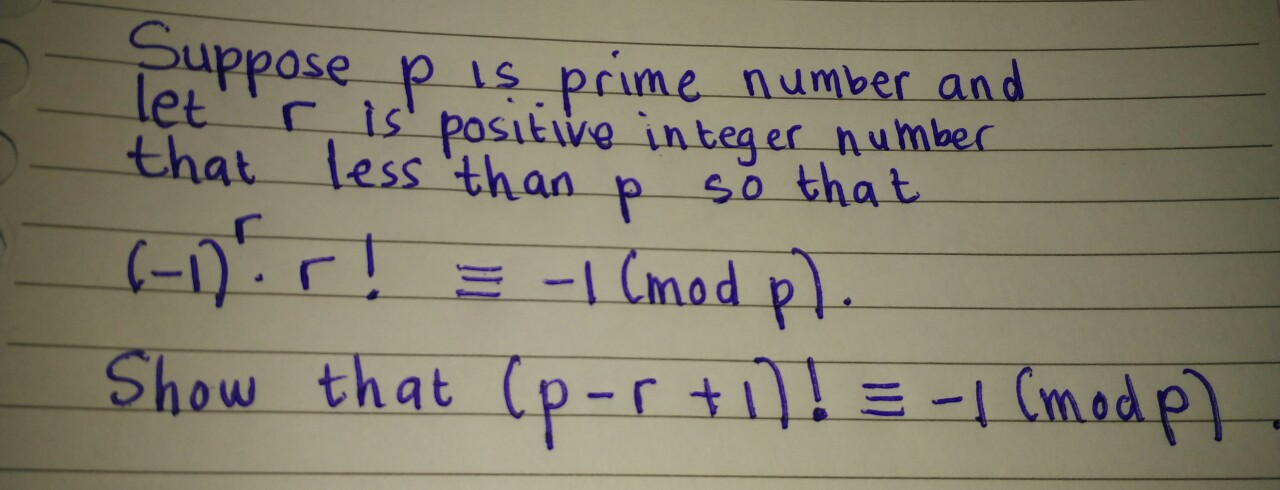Hmmm. Let's check #p=5, r=3.# because #(-1)^3 \ 3! = -6 = -1 mod 5 quad sqrt#
# (5-3+1)! =3! =1 mod 5 quad # WRONG
I think the correct formulation is
#(p-r-1)!equiv 1 (mod p)#
This looks like it's related to Wilson's Theorem. A positive integer #n# is a prime if and only if #(n-1) ! equiv -1 (mod n)#.
I'll give an informal justification for Wilson. For composite #n# the factorial will contain a pair of factors that multiply to #n# so the whole thing is zero so can't be #-1#.
For prime #n# we have a finite field. Multiplicative inverses in a finite field come in pairs; the only cases you're your own inverse is #a=1/a# or #a^2=1# or #a=pm 1#. So #(n-1)! = (n-1)(n-2)! = -(n-2)!# and #(n-2)!# has all the pairs of inverses, and only pairs of inverses (and a lonely factor of one, which makes no difference), so is #1# so the whole thing is #-1.#
Back to our problem.
We have #r < p # or #r le p-1 #. We can try to expand #(p-1)!
=-1# with one factor #(p-r-1)!# and see what happens. Working #(mod p\ )#
# (p-1) ! = (p-1)(p-2)...(p-r) \ (p-(r+1))! #
#-1 equiv (-1)(-2)...(-r) cdot (p-r-1)! #
#-1 equiv (-1)^{r} \ r! \ (p-r-1)! #
# -1 equiv -(p-r-1)! #
# (p-r-1)! equiv 1 quad mod p#