Question

(x+1)(x+2)(x+3)(x+4)-3?

Answer 1

`x^4+10x^3+35x^2+50x+21`

Explanation:

So let do the first two binomial first.

`(x+1)(x+2)`
`x^2+2x+1x+2` - FOIL Method

FOIL stands for:
F - First
O - Outside
I - Inside
L - Last

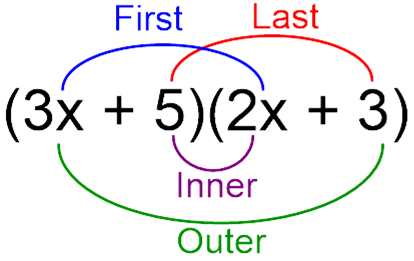
So after we FOIL, combine any like terms we have.

`x^2+3x+2`

Now let use the FOIL method for the remaining two binomial.

`(x+3)(x+4)`
`x^2+3x+4x+12`

Now we will combine the like terms.

`x^2+7x+12`

So now we can use the distributive property for both of these quadratic trinomial. We also have to bring down the 3.

`(x^2+3x+2)` `(x^2+7x+12)-3`
`x^4+7x^3+12x^2+3x^3+21x^2+36x+2x^2+14x+24-3`

Now we can combine the like terms. It is always a good idea to double check your work at this point to ensure you didn't forget to do something in the distributive property. When using the distributive property for this type of work, ensure that you do not multiply the exponents as that is not how it work. As the product rule of exponent states, you add exponent together.

So combining like terms give you this:

`x^4+10x^3+35x^2+50x+21`