Question

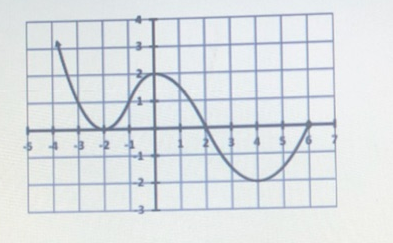
`y=f(x)` is given. Graph, `y=f(3x)-2` and `y=-f(x-1)`?

Answer 1

Don't have graph paper handy - so I hope that the description helps!

Explanation:

For `y=f(3x)-2` first squeeze the given graph along the `x` axis by a factor of 3 (so that the left hand minimum, say, occurs at `x=-2/3` ), and then push the whole graph down by 2 units. Thus the new graph will have a minimum at `x = -2/3` with a value of `y= -2`, a maximum at `(0,0)` and another minimum at `(4/3, -4)`

For `y=-f(x-1)` first shift the graph 1 unit to the right , then flip it upside down! So, the new graph will ave two maxima at `(-1,0)` and `(5,2)` and a minimum at `(1,-2)`

Answer 2

Here is a more detailed explanation

Explanation:

The problems are special cases of a more general problem :

Given the graph for `y=f(x)`, what is the graph of `y = a f(b x+c)+d` ?

(the first one is for `a=1, b= 3, c=0, d=-2`, while the second one is for `a=-1, b=1,c=-1, d=0` )

I will try to explain the answer in steps, by tackling the problem one step at a time. It will be a pretty long answer - but hopefully the general principle will be clear by the end of it.

For illustration I'll use a particular curve that I am showing below, but the idea will work in general.

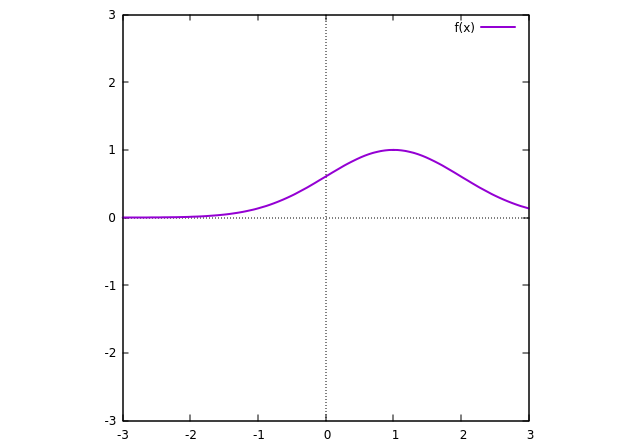
(If anyone is interested, the function that is being plotted here is `f(x) = exp(-{(x-1)^2}/2)`

1) Given the graph for `y=f(x)`, what is the graph of `y = f( x)+d` ?

This one is easy - all you have to do is note that if `(x,y)` is a point on the first graph, then `(x,y+d)` is a point on the second. This means that the second graph is higher than the first by a distance `d` (of course, if `d` is negative, it is lower than the first graph by `|d|` ).

So, the graph of `y=f(x)+1` will be

As you can see, the graph for `y = f(x)+1` (the solid purple line) is obtained by simply pushing the graph for `y=f(x)` (the gray dashed line) up by one unit.

The graph for `y=f(x)-1` can be found by pushing the original graph down by one unit :

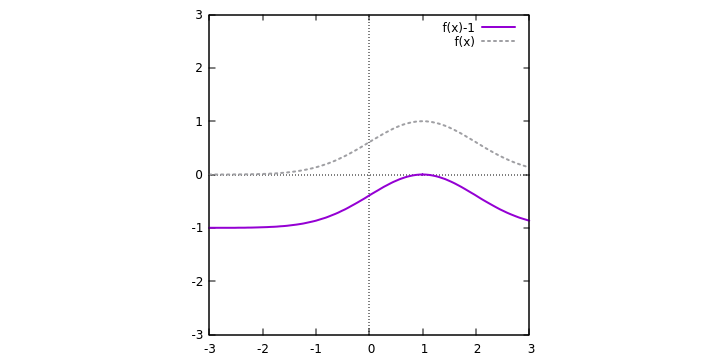
2) Given the graph for `y=f(x)`, what is the graph of `y = f( x+c)` ?

It is easy to see that if `(x,y)` is a point on the `y=f(x)` graph, then `(x-c,y)` will be a point on the `y = f(x+c)` graph. This means that you can get the graph of `y = f( x+c)` from the graph of `y = f( x)` simply by shifting it to the left by `c` (of course, if `c` is negative, you must shift the original graph by `|c|` to the right.
As an example, the graph for `y=f(x+1)` can be found by pushing the original graph to the left by one unit :

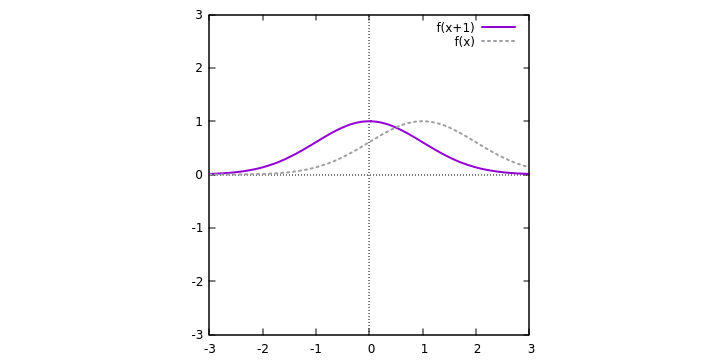
while that for `y=f(x-1)` involves pushing the original graph to the right by one unit :

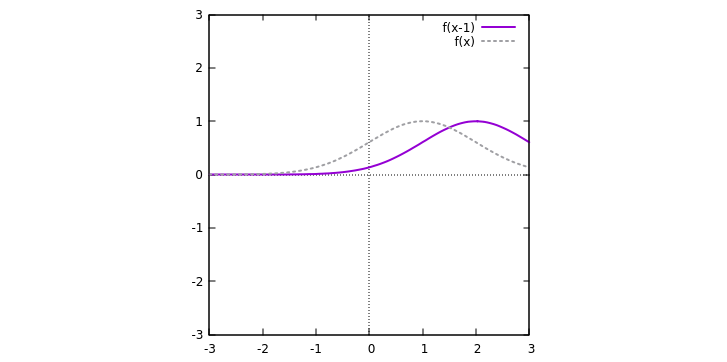
3) Given the graph for `y=f(x)`, what is the graph of `y = f( bx)` ?

Since `f(x) = f(b times x/b)` it follows that if `(x,y)` is a point on the `y = f(x)` graph, then `(x/b , y)` is a point on the `y=f(bx)` graph.

This means that the original graph has to be squeezed by a factor of `b` along the `x` axis. Of course, the squeezing by `b` is really a stretching by `1/b` for the case where `0 < b <1`

The graph for `y=f(2x)` is

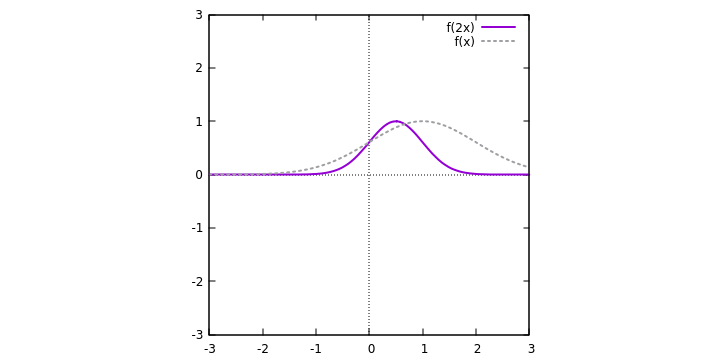
Note that the while the height stays the same at 1, the width shrinks by a factor of 2. In particular, the peak of the original curve has shifted from `x=1` to `x=1/2`.

On the other hand, the graph for `y=f(x/2)` is

Note that this graph is twice as broad (squeezing by `1/2` being the same as stretching by a factor of 2), and the peak has also moved from `x=1` to `x=2`.

A special mention must be made of the case where `b` is negative. It is best perhaps to then think of this as a two-step process

• First find the graph of `y=f(-x)`, and then
• squeeze the resulting graph by `|b|`

Note that for each point `(x,y)` of the original graph, the point `(-x,y)` is a point on the graph of `y=f(-x)` - so the new graph can be found by reflecting the old one about the `Y` axis.

As an illustration of the two step process, consider the graph of `y=f(-2x)` shown below :

Here the original curve, that for `y=f(x)` is first flipped about the `Y` axis to get the curve for `y=f(-x)` (the thin cyan line). This is then squeezed by a factor of `2` to get the curve for `y=f(-2x)` - the thick purple curve.

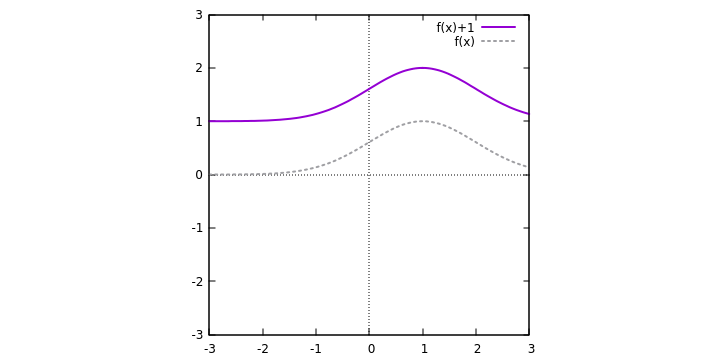
4) Given the graph for `y=f(x)`, what is the graph of `y = af( x)` ?
The pattern is the same here - if `(x,y)` is a point on the original curve then `(x,ay)` is a point on the graph of `y=af(x)`

This means that for a positive `a`, the graph gets stretched by a factor of `a` along the `Y` axis. Again, a value of `a` between 0 and 1 means that instead of being stretched, the curve will actually be squeezed by a factor of `1/a` along the `Y` axis.

The curve below is for `y = 2f(x)`

Note that the while the peak is at the same value of `x` - its height has doubled to 2 from 1. Of course it is not the peak only that has been stretched - the `y` coordinate of every point of the original curve has been doubled to get the new curve.

The figure below illustrates the squeezing that occurs when `0<a<1`

Once again, the case for `a<0` takes special care - and it is better if you do this in two steps

1. First flip the curve upside down about the `X` axis to get the curve for `y=-f(x)`
2. Stretch the curve by `|a|` along the `Y` axis.

The curve for `y=-f(x)` is

while the picture below illustrates the two steps involved in drawing the curve for `y = -2f(x)`

Putting it all together

Now that we have gone through the individual steps, let us put them all together! The procedure for drawing the curve for

`y = a f(bx+c)+d`

starting from that of `y=f(x)` is essentially composed of the following steps

1. Plot the curve of `y=f(x+c)` : shift the graph by a distance `c` to the left
2. Then plot that of `y = f(bx+c)` : squeeze the curve that you get from step 1 in the `X` direction by the factor `|b|`, (first flipping it about the `Y` axis if `b<0`)
3. Then plot the graph of `y=af(bx+c)` : scale the curve that you got from step 2 to by a factor of `a` in the vertical direction.
4. Finally push the curve that you obtain in step 3 up by a distance `d` to get the final result.

Of course you need to carry out all four steps only in extreme cases - often a smaller number of steps will do! Also, the sequence of steps is important.
In case you are wondering, these steps follow from the fact that if `(x,y)` is a point on the `y=f(x)` graph, then the point
`({x-c}/b,ay+d)` is on the `y=af(bx+c)+d` graph.

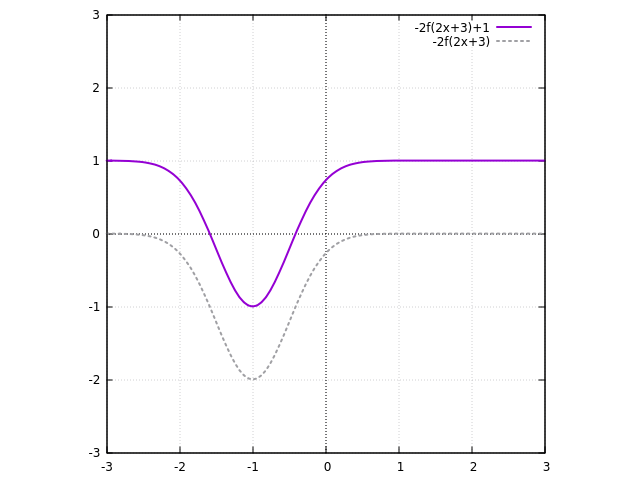
Let me illustrate the process by an example with our function `f(x)`. Let us try to construct the graph for `y = -2f(2x+3)+1`

First - the shift to the left by 3 units

Then : squeeze by a factor of 2 along the `X` axis

Then, flipping the graph over about the `X` axis and then scaling by a factor of 2 along `Y`

Finally, shifting the curve up by 1 unit - and we are done!