You flip a coin and roll a die. What is the probability that you obtain a head on the coin and a 2 on the die?
1 Answer
Feb 12, 2015
The probability that you obtain a head on the coin and a 2 on the die is
Assuming the coin and the die are unbiased:
the probability of obtaining a head on the coin is
and
the probability of obtaining a 2 on die is
These are independent events. What happens with the coin does not effect what happens with the die.
Therefore the probability of the combined outcome is the product of their individual probabilities.
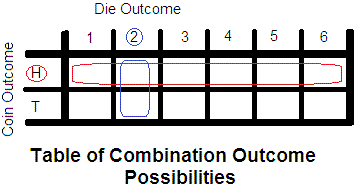
From the above we can see that there are
The desired outcome (the intersection of the Die Outcome
Therefore the probability of the desired outcome is
