You put in a flower bed measuring 20 feet by 30 feet. To finish the project you are putting in a uniform border of bark around the outside of the rectangular garden. You have enough bark to cover 336 square feet. How wide should the border be?

Question

I know the equation I should be using is [(20+x)(30+x)]-(20*30)=x

2808 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-04-25T03:09:13

The border of bark is #4#ft wide

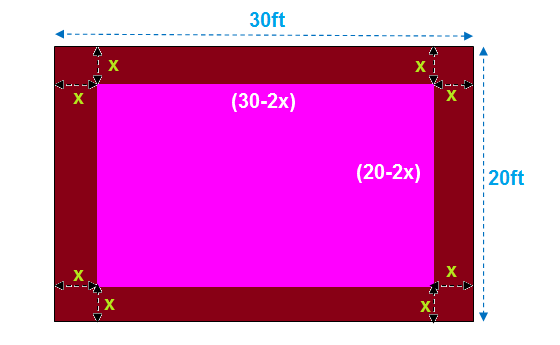
enter image source here

Length of the rectangular flower bed including border is #30ft#

Breadth of the rectangular flower bed including border is #20ft#

Let the border of bark be #x#ft wide.

So excluding border

length becomes #(30-2x)# ft

and breadth becomes #(20-2x)# ft

Given area of the border #336ft^2#

So we have

#(20*30)-(20-2x)(30-2x)=336#

#=>20*30-(20*30)+100x-4x^2=336#

#=>100x-4x^2=336#

#=>x^2-25x+84=0#

#=>x^2-21x-4x+84=0#

#=>x(x-21)-4(x-21)=0#

#=>(x-21)(x-4)=0#

So #x=4# ft

#x=21# not possible