You roll 2 dice. What is the probability that the sum of the die is even and one shows a 3?

Question

3809 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-01-31T06:13:53

#=5/36#

we also can write as
#(1,1),...(1,6)#,
#(2,1),...(2,6)#,
#(3,1),...((3,6)#,
#(4,1),...(4,6)#,
#(5,1),...(5,6)#, and
#(6,1),...(6,6)#

and it total is #36#.
therefore #n(xi) =36#

Let say that #A# is an outcome for which a 3 must one show and their sum is even are (#3,1),(3,3),(3,5), (1,3) and(5,3)#, therefore #n(A) = 5#

Probability A =#(n(A))/(n(xi))#

#=5/36#

Answer 2 · 2017-01-31T06:21:36

#p=5/36#

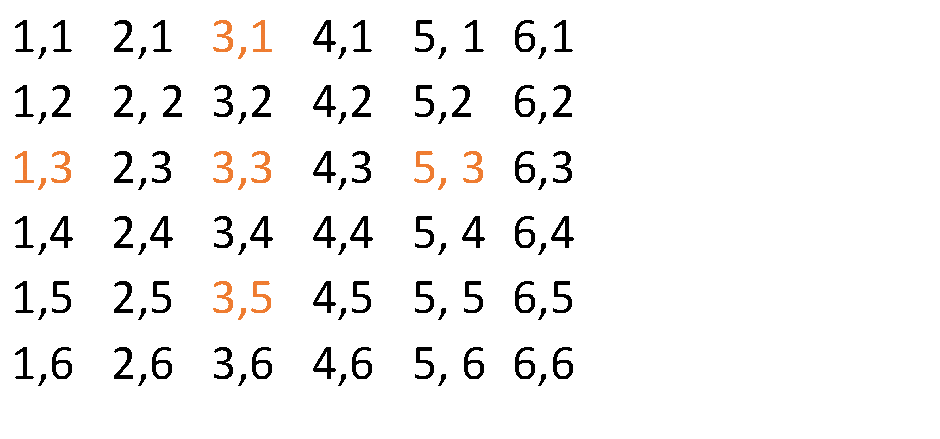
enter image source here

There are 36 outcomes. Of which 5 are favourable.

Probability = Number of favourable outcomes)/ Total number of outcomes

#p=5/36#