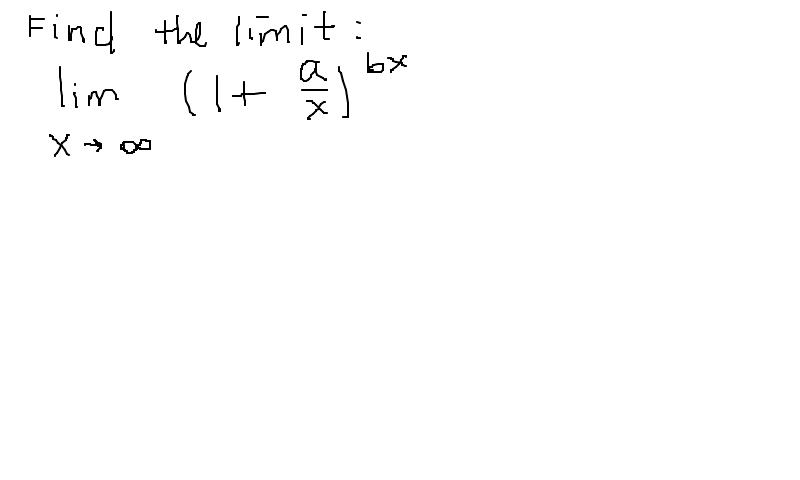What is the limit as x approaches infinity of #(1+a/x)^(bx)#?
1 Answer
By using logarithm and l'Hopital's Rule,
By using the substitution
By using logarithmic properties,
By l'Hopital's Rule,
Hence,
(Note:
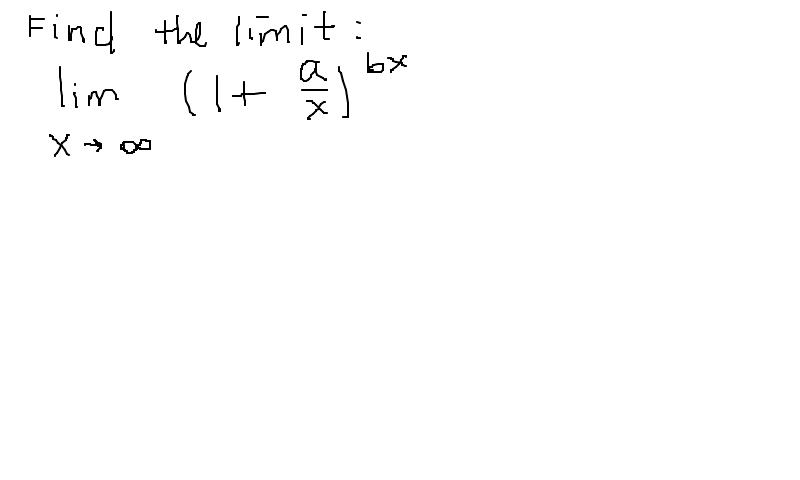
By using logarithm and l'Hopital's Rule,
By using the substitution
By using logarithmic properties,
By l'Hopital's Rule,
Hence,
(Note: