Question #bab32
3 Answers
When an object is dropped so that only the force of gravity is acting on it, the symbol for acceleration becomes
Example 1. Dropping a book from a height of
How long will it take the book to land, and what will its final velocity be?
Known/Given:
Unknown:
time,
final velocity
Equations:
Solution:
First, determine the final velocity of the book when it lands using the kinematic equation
(Remember that a square root is + or -, and the downward motion is negative.)
Now determine the time it takes for the book to land using the equation
Since
So, if you drop a book from a height of
Example 2. Throwing a book down from a height of
Lets say you threw a book down with an initial velocity of
How long will it take the book to land, and what will its final velocity be?
Known/Given:
Unknown:
time,
final velocity
Equations:
Solution:
First, determine the final velocity of the book when it lands using the kinematic equation
(Again, remember that a square root is + or -, and here the downward motion is negative.)
Now determine the time it takes the thrown book to land using the equation
So a book thrown down from a height of
Yes. When an object is dropped, its initial velocity is zero and its acceleration is that of gravity, which is
There are four kinematic equations that are used to study motion in one direction. .
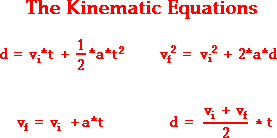
Two of these equations will be used to test how fast an object falls, and its final velocity.
Note: When an object is dropped so that only the force of gravity is acting on it, the symbol for acceleration becomes
When an object is dropped so that only the force of gravity is acting on it, the symbol for acceleration becomes
Example 1. Dropping a book from a height of
How long will it take the book to land, and what will its final velocity be?
Known/Given:
Unknown:
time,
final velocity
Equations:
Solution:
First, determine the final velocity of the book when it lands using the kinematic equation
(Remember that a square root is + or -, and the downward motion is negative.)
Now determine the time it takes for the book to land using the equation
Since
So, if you drop a book from a height of
Example 2. Throwing a book down from a height of
Lets say you threw a book down with an initial velocity of
How long will it take the book to land, and what will its final velocity be?
Known/Given:
Unknown:
time,
final velocity
Equations:
Solution:
First, determine the final velocity of the book when it lands using the kinematic equation
(Again, remember that a square root is + or -, and here the downward motion is negative.)
Now determine the time it takes the thrown book to land using the equation
So a book thrown down from a height of
Yes. When an object is dropped, its initial velocity is zero and its acceleration is that of gravity, which is
There are four kinematic equations that are used to study motion in one direction. .
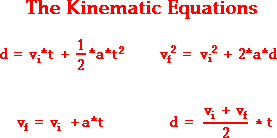
Two of these equations will be used to test how fast an object falls, and its final velocity.
Note: When an object is dropped so that only the force of gravity is acting on it, the symbol for acceleration becomes
Example 1. Dropping a book from a height of
How long will it take the book to land, and what will its final velocity be?
Known/Given:
Unknown:
time,
final velocity
Equations:
Solution:
First, determine the final velocity of the book when it lands using the kinematic equation
(Remember that a square root is + or -, and the downward motion is negative.)
Now determine the time it takes for the book to land using the equation
Since
So, if you drop a book from a height of
Example 2. Throwing a book down from a height of
Lets say you threw a book down with an initial velocity of
How long will it take the book to land, and what will its final velocity be?
Known/Given:
Unknown:
time,
final velocity
Equations:
Solution:
First, determine the final velocity of the book when it lands using the kinematic equation
(Again, remember that a square root is + or -, and here the downward motion is negative.)
Now determine the time it takes the thrown book to land using the equation
So a book thrown down from a height of

