Question

How do I estimate the area under the graph of f(x) = `3 cos(x)` from `x=0` to `x=pi/2` using left and right endpoint methods?

Answer 1

You'll need a value for `n` to actually get an answer, but here's the method:

For your question `f(x)=3cos(x)`,
`a=0`, and `b=pi/2`

Find `Delta x = (b-a)/n =(pi/2-0)/n=pi/(2n)`

Find all endpoints: start at `a` and successively add `Delta x` until you get to `b`:

`0, pi/(2n), (2pi)/(2n), (3pi)/(2n), * * * , ((n-1)pi)/(2n), (npi)/(2n)=pi/2`

Each rectangle has ares base times height, which will be `Delta x` times `f` at an enpoint

To use left endpoints , delete the last endpoint, above, because it is not a left endpoint

Rectangle 1 has area `Delta x *f(0) = (pi/(2n))3cos(0)`

Rectangle 2 has area `Delta x *f(pi/(2n)) = (pi/(2n))3cos(pi/(2n))`

Rectangle 3 has area `Delta x *f((2pi)/(2n))=(pi/(2n))3cos(2pi/(2n))`

Rectangle 4 has area `Delta x *f((3pi)/(2n))=(pi/(2n))3cos(3pi/(2n))`

And so on up to

Rectangle n has area `Delta x *f(((n-1)pi)/(2n))=(pi/(2n))3cos(((n-1)pi)/(2n))`

Do the arithmetic and add the areas.

For right endpoints delete the case `x=0` and add the case `x= pi/2`

`(pi/(2n))3cos(pi/(2n))+pi/(2n))3cos(2pi/(2n)+(pi/(2n))3cos(3pi/(2n))+ * * * +(pi/(2n))3cos((pi)/2)`

Answer 2

You can divide the range `0` to `pi/2` into a few rectangular strips and using left and right edges (endpoints) multiplied by the width of each strip calculate a minimum and a maximum area.

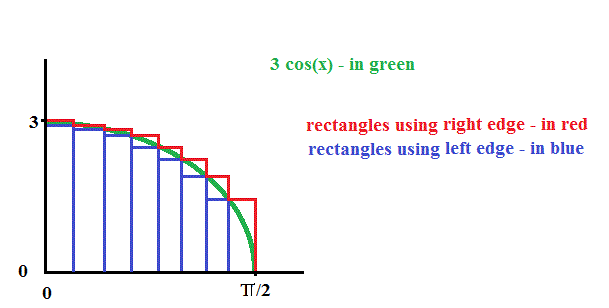
Even for only a few rectangular strips the calculations can become tedious and I would recommend using a computer in some way.

Here is a display from an Excel spreadsheet with 4 rectangular strips:

Notice with this few rectangles the difference between minimum and maximum values is probably unacceptable.

If you can program in some simple language, it is fairly easy to write code that will repeatedly divide the rectangular strips into finer widths until the minimum and maximum areas are very close together.

For example, with a maximum allowable difference set at 0.0001, a small Basic program gave the result:
Integral value of 3 Cos(x) for x from 0 to pi/2 falls between 2.99996405 and 3.00003595