I would say that the difference in boiling points is due to an increase in external pressure.
A liquid boils when its vapor pressure is equal to the external pressure - more often than not, this is the atmospheric pressure.
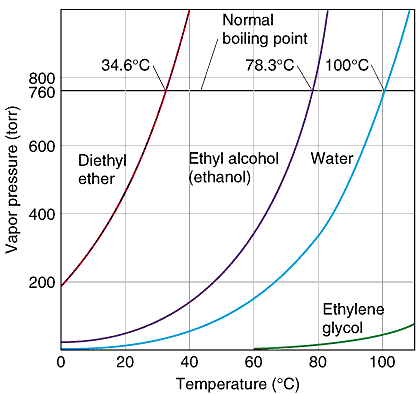
So, at normal atmospheric pressure, or 1 atm, ethanol boils at #78.3^@"C"#. In this case, the heat you provide is enough to make the vapor pressure equal the atmospheric pressure #-># boiling takes place.
If the atmospheric pressure is higher, the vapor pressure will have to be higher as well, since boiling occurs only when vapor pressure equals atmospheric pressure.
As a result, you'll need to supply more heat to the sample, which means it will boil at a higher temperature.
In your case, the first sample boils at #79^@"C"#, which means that the atmospheric pressure is very, very close to 1 atm, while the second sample boils at #81^@"C"#, which implies that the atmosperic pressure is a little higher than 1 atm.
SIDE NOTE
You can determine this mathematically by using the Clausius-Clapeyron equation
#ln(P_2/P_1) = (DeltaH_"vap")/R * (1/T_1 - 1/T_2)#, where
#P_1#, #P_2# - the vapor pressure at boiling point #79^@"C"# and #81^@"C"#, respectively;
#DeltaH_"vap"# - the enthalpy of vaporization for ethanol - #"38.56 kJ/mol"#;
#T_1#, #T_2# - the boiling points of the first and of the second sample - expressed in Kelvin.
For the sake of argument, let's assume that, at 1 atm, ethanol boils at #79^@"C"#. Since #T_2# is bigger than #T_1#, you'd expect #P_2# to be bigger than #P_1#. Indeed it is
#ln(P_2/1) = (38560cancel("J")/cancel("mol"))/(8.314cancel("J")/(cancel("K")cancel("mol"))) * (1/(352.15) - 1/(354.15))cancel("K")#
#ln(P_2) = 0.06917 => P_2 = "1.072 atm"#
Higher atmospheric pressure, higher boling point.


