How do you find equation of tangent to circle #x^2 + y^2 = 25# at the point (-3, 4)?

Question

52048 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-04-14T14:45:40

The answer is: #y=3/4x+25/4#.

The circle is not a function, so we have to divide it in two half.

#y=+-sqrt(25-x^2)#.

We need the above semicircle, because the point is in the second quadrant. So the function we need is:

#y=+sqrt(25-x^2)#.

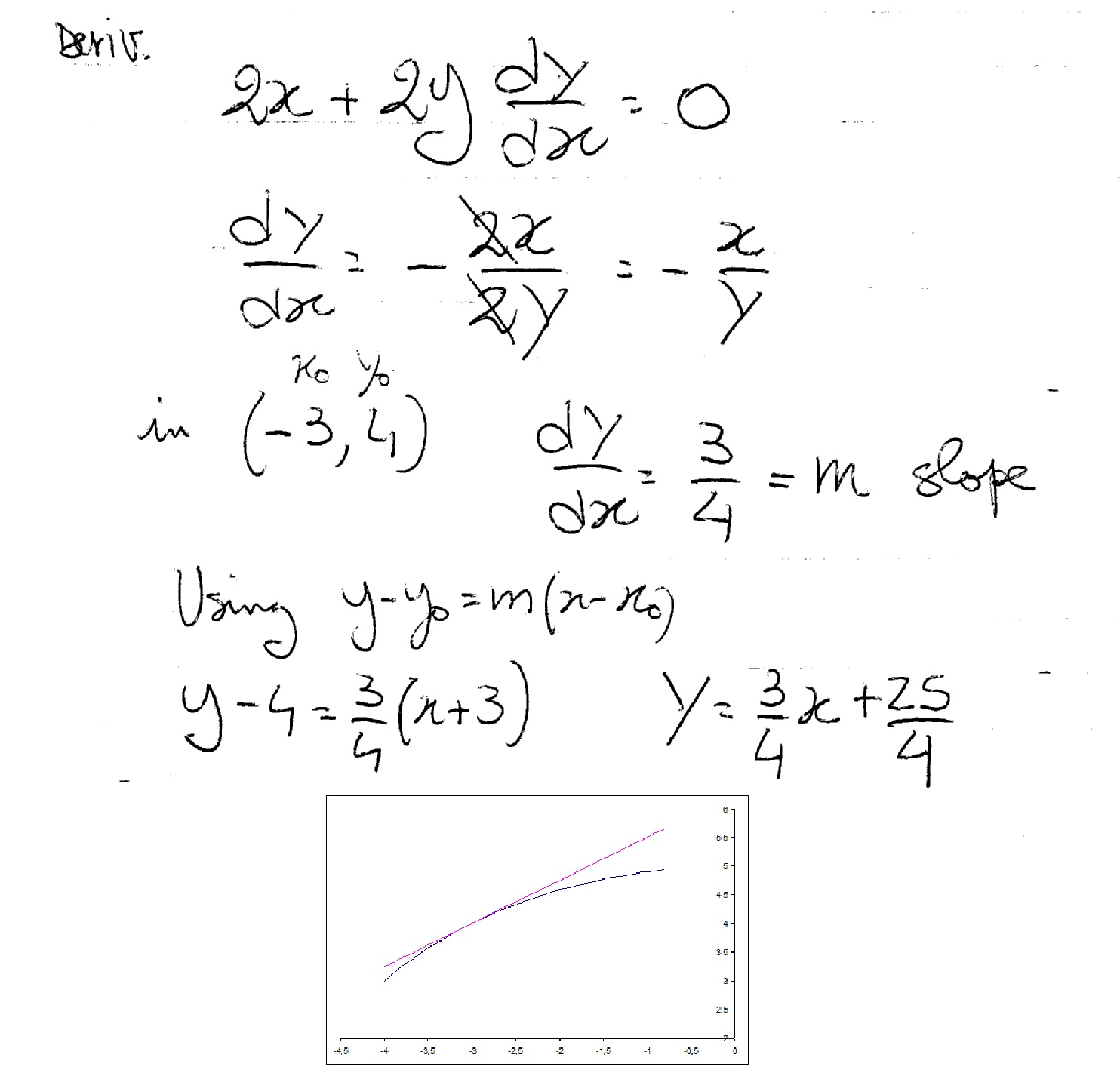
Its derivative is:

#y'=1/(2sqrt(25-x^2))*(-2x)=-x/sqrt(25-x^2)#.

The slope in the point #(-3,4)# is:

#y'(-3)=-(-3)/sqrt(25-9)=3/4#.

So the tangent line is:

#y-4=3/4(x+3)rArry=3/4x+25/4#.

Answer 2 · 2015-04-14T14:48:03

Have a look:
enter image source here