I assume in your question that you desire to find a value cc between 0 and 4 so that f'(c)=\frac{f(4)-f(0)}{4-0}=\frac{2-0}{4-0}=\frac{1}{2}. Since f'(c)=1-\frac{1}{2}c^{-1/2}, that means you want to solve the equation 1-\frac{1}{2}c^{-1/2}=\frac{1}{2} for c. This equation can be rearranged to say that \frac{1}{2c^{1/2}}=\frac{1}{2} so that c^{1/2}=1. This tells you that c=1.
A comment about what we are really doing here: we are not really "using" the Mean Value Theorem to solve anything. Rather, we are solving an algebra equation related to the instantaneous rate of change f'(c) and the average rate of change \frac{f(4)-f(0)}{4-0} to find the value of c that is guaranteed to exist by the Mean Value Theorem over the interval [0,4] (a value of c where the instantaneous rate of change equals the average rate of change). In effect, we are just illustrating the truth of the theorem, not using it.
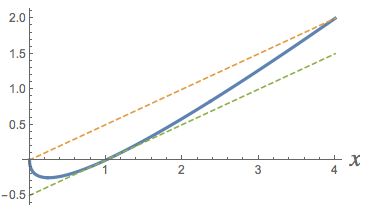
Here's a picture of the situation in this problem. Note that the two dashed lines have equal slopes: