The derivative is #1/{\sqrt{2x}\sqrt(1-2x)}#
Let #y=arcsin\sqrt{2x}#
The goal is to solve for #{dy}/{dx}#. Take #sin# of each side of the bove equation and get,
#sin(y)=\sqrt{2x}#
Take the derivative of each side with respect to #x#
#cos(y){dy}/{dx}=1/\sqrt{2x}#
#{dy}/{dx}=1/{\sqrt{2x}cos(y)}#
We need to know what #cos(y)# is. Use #sin(y)=\sqrt{2x}/1=\text{opposite}/\text{hypotenuse}# to get the triangle below.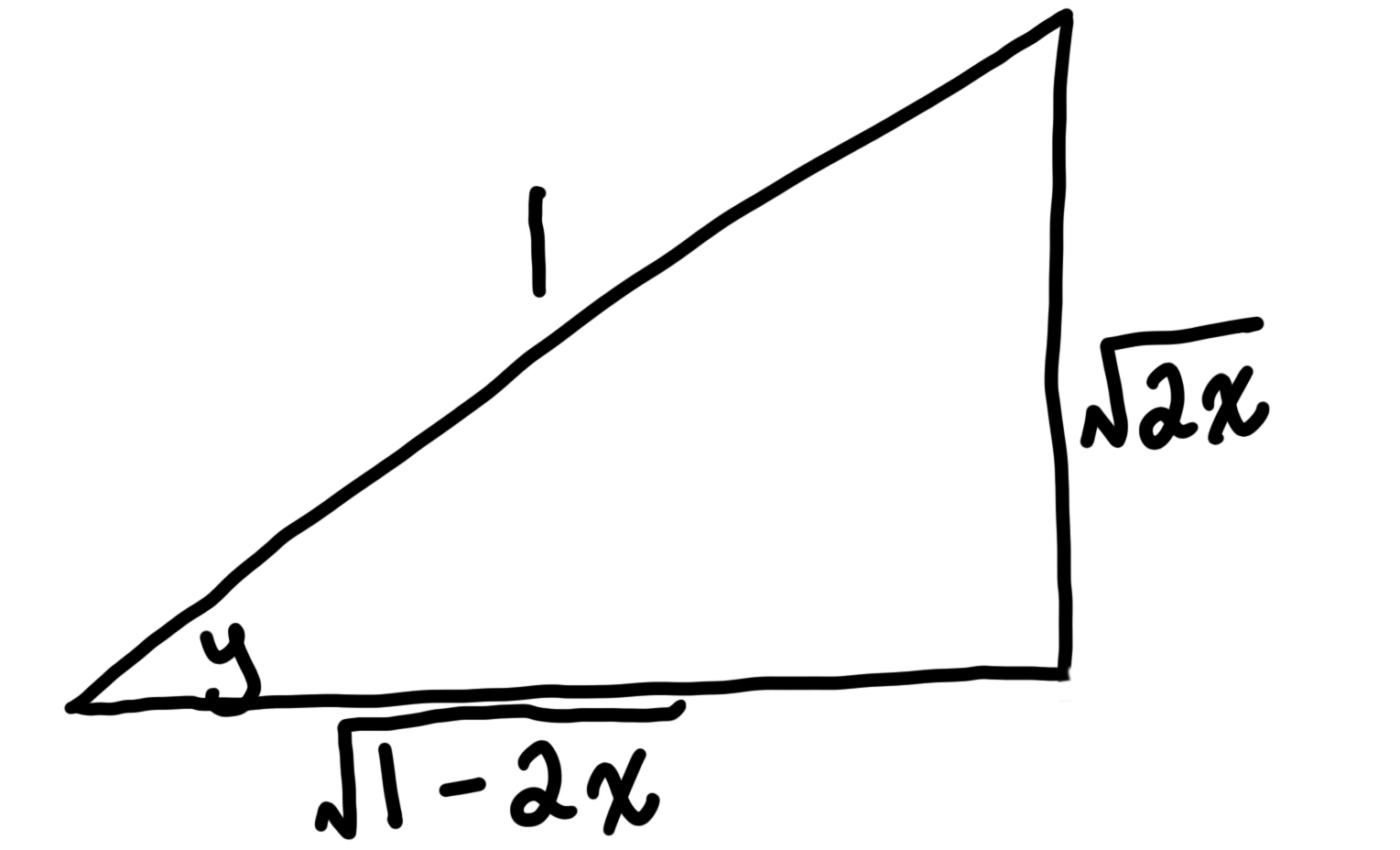
From the diagram #cos(y)={\sqrt{1-2x}}/1#. Substitute this into the #{dy}/{dx}# expression to get,
#{dy}/{dx}=1/{\sqrt{2x}\sqrt(1-2x)}#
Alternatively, use the chain rule.
Given,
#d/{dz}[arcsin(z)]=1/\sqrt{1-z^2}#
Let #z=\sqrt{2x}#
#d/dx[arcsin(\sqrt{2x})]=d/dz[arcsin(z)]dz/dx#
Substitute #z=\sqrt{2x}# to get the same answer as before
#d/dx[arcsin(\sqrt{2x})]=1/{\sqrt{2x}\sqrt(1-2x)}#

