Question #aabf4
1 Answer
Use a proof by contradiction to show that no other line segment can be shorter than the perpendicular one.
Explanation:
Take
We're going to use proof by contradiction, meaning that we are going to assume the opposite of the statement we are trying to prove and prove that it is impossible.
Assume that there is a different line segment from
This creates a right triangle
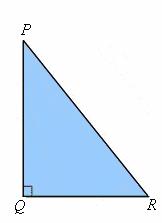 http://www.icoachmath.com
http://www.icoachmath.com
Since we have a right triangle, we know that we can use the Pythagorean theorem,
Since
But, if each side is positive,
Since we have proved that it is impossible for there to be a shorter line segment than the perpendicular line segment, we have proved that the perpendicular line segment is the shortest one.

