How do you find the integral #(ln x)^2#?
3 Answers
I found:
Explanation:
I would try using Substitution and By Parts (twice):
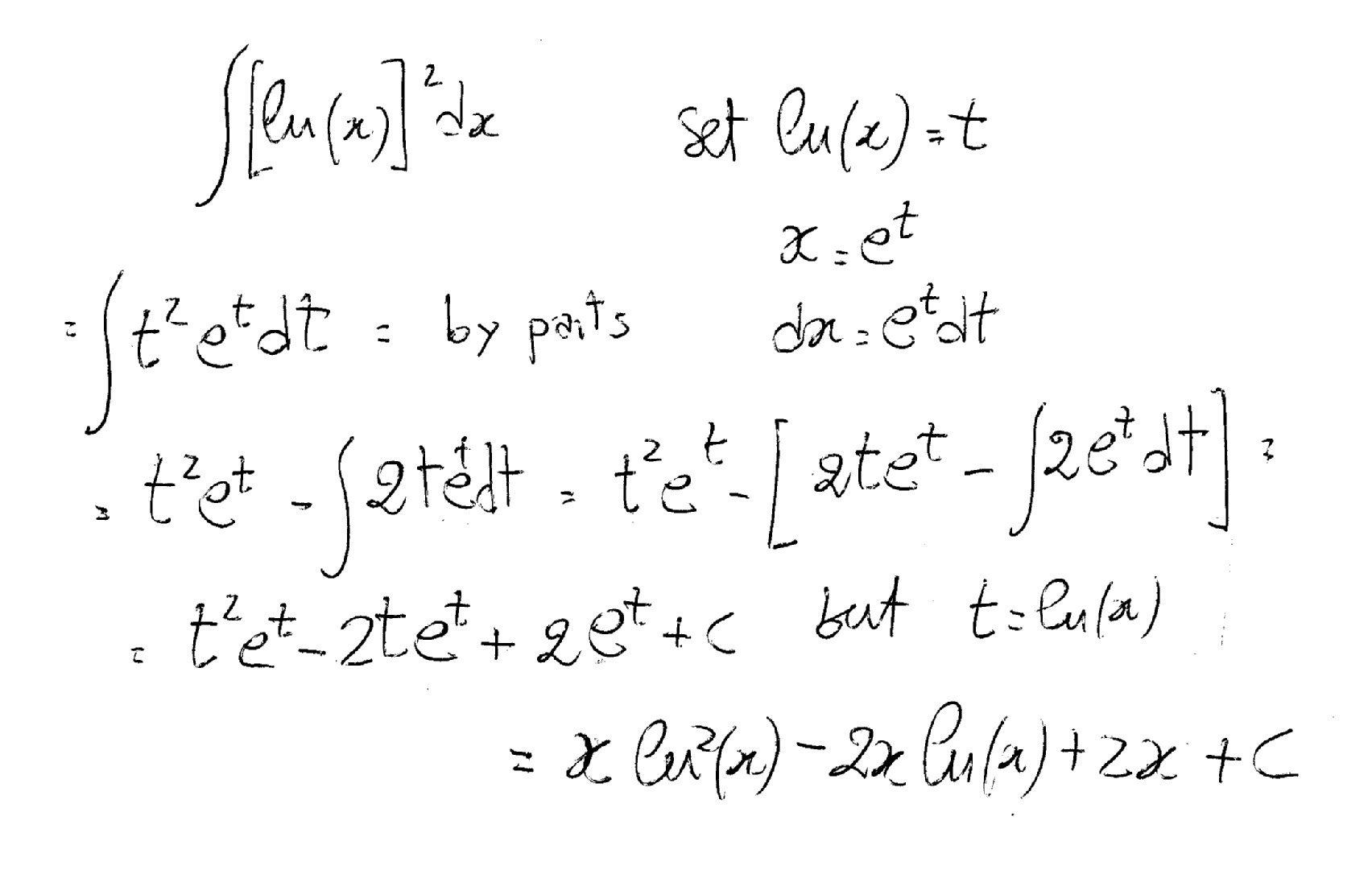
I get the same answer as Gio,
But the details of my solution are different.
Explanation:
Use integration by parts:
Let
# = x (lnx)^2 -2 int lnx dx#
# = x (lnx)^2 -2 [ xlnx - x]+C#
# = x(lnx)^2-2xlnx+2x+C#
Note
If you don't know
General note
In general to integrate:
As funny as it sounds, I'm just going to do it like this. It's how I did it the first time I've seen this one. Let:
To do
Let:
Anyways, continuing on:
Cool, still got the same answer.



