Question

Calculate the enthalpy of reaction for the reaction `"CH"_3"COOH" + "H"_2"O" -> "CH"_3"CH"_2"OH" + "O"_2`?

Answer 1

Well, you could just look up the standard enthalpies of formation, although you didn't specify at what temperature or pressure, and what phases. My assumption though is that you're at STP.

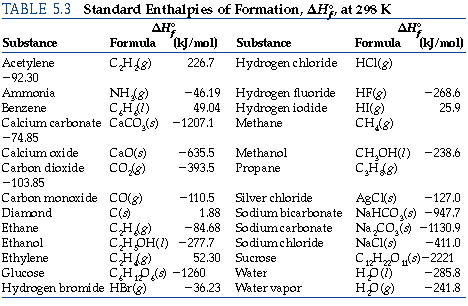
Acetic acid is here:
https://en.wikipedia.org/wiki/Acetic_acid_%28data_page%29

Its liquid `Delta_fH = -483.5 (kJ)/(mol)`
Its gaseous `Delta_fH = -438.1 (kJ)/(mol)`

I know that the ethanol is a liquid at STP, and oxygen is a gas at STP (it's also in its elemental state, so its enthalpy of formation is 0). Water might be a gas, or a liquid, but you have to know which one. Usually if it's a product, it's ambiguous without specifying...

I'll just give all four possibilities.

`Delta_(rxn)H = nu_(P_i)sum_(P_i)Delta_fH_(P_i) - nu_(R_i)sum_(R_i)Delta_fH_(R_i)`

where `P_i` is each of the products, `R_i` is each of the reactants, and `nu` is the stoichiometric coefficient.

`= [1*Delta_fH_("Ethanol") + 1*Delta_fH_(O_2)] - [1*Delta_fH_("Acetic Acid") + 1*Delta_fH_(H_2O)]`

1)
`= [(1)(-277.7) + (1)(0)]-[(1)(-483.5)(l) + (1)(-285.8)(l)]`

`= -277.7 + 483.5 + 285.8 = 491.6 (kJ)/(mol)`

2)
`= [(1)(-277.7) + (1)(0)]-[(1)(-483.5)(l) + (1)(-241.8)(g)]`

`= -277.7 + 483.5 + 241.8 = 447.6 (kJ)/(mol)`

3)
`= [(1)(-277.7) + (1)(0)]-[(1)(-438.1)(g) + (1)(-285.8)(l)]`

`= -277.7 + 438.1 + 285.8 = 446.2 (kJ)/(mol)`

4)
`= [(1)(-277.7) + (1)(0)]-[(1)(-438.1)(g) + (1)(-241.8)(g)]`

`= -277.7 + 438.1 + 241.8 = 402.2 (kJ)/(mol)`

And then, considering how there is no `CO_2`, this is likely a radical reaction instead of a combustion reaction (elemental oxygen is triplet oxygen, which is paramagnetic, single-bonded, and has radical electrons). Radical reactions tend to be exothermic, so the results are negative. My way uses triplet oxygen, but it should probably be singlet oxygen, which has a double bond.

The accepted answer is `-494 (kJ)/(mol)`, and using singlet oxygen would probably account for that, since breaking an extra bond would make the resultant enthalpy of formation more negative.

Answer 2

You can find the enthalpy change for your reaction by using bond enthalpies.

Explanation:

The enthalpy change for a reaction can also be calculate by using bond enthalpies. In any chemical reaction, some bonds are being broken and others are being formed.

More specifically, the bonds of the reactants are being broken and the bonds of the products are being formed.

The enthalpy change of the reaction will be the difference between the energy that's needed to break the bonds of the reactants and the energy that's given off when the bonds of the products are formed.

`DeltaH_"rxn" = sum(DeltaH_"broken") - sum(DeltaH_"formed")`

In order to get an idea about what bonds are being broken and what bonds are being formed, take a look at the Lewis structures of the specis that take part in th reaction

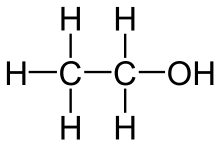
So, for ethanol, you need to break

• five `"C"-"H"` bonds;
• one `"C"-"C"` bond;
• one `"C"-"O"` bond;
• one `"O"-"H"` bond.

For diatomic oxygen, you just need to break one `"O"="O"` bond.

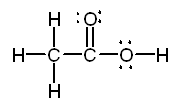
For acetic acid, you need to form

• three `"C"-"H"` bonds;
• one `"C"-"C"` bond;
• one `"C"-"O"` bond;
• one `"O"-"H"` bond;
• one `"C"="O"` bond.

For water, you need to form two `"H"-"O"` bonds.

Here's a table containing the bond enthalpies you need for your reaction.

Since you're dealing with 1 mole of each compound, you can go ahead and use the bond enthlpies in kJ, rather than kJ per mole. So, the enthalpy change for your reaction will be

`DeltaH_"rxn" = (5 * 413"kJ" + 1 * "348 kJ" + 1 * "358 kJ" + 1 * "463 kJ" + 1 * "495 kJ") - (3 * "413 kJ" + 1 * "348 kJ" + 1 * "358 kJ" + 3 * "463 kJ" + 1 * "799 kJ")`

`DeltaH_"rxn" = "3729 kJ" - "4133 kJ" = color(green)(-"404 kJ")`

The accepted value for the enthalpy change of this reaction is actually -494 kJ, so double-check my calculations!