Question

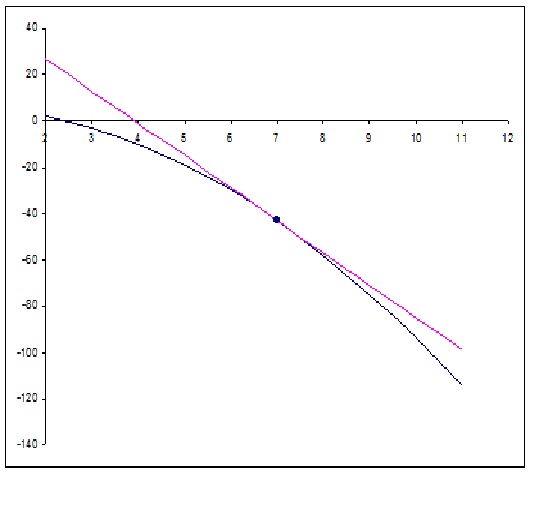
How do you find the slope and tangent line to the curve `y=6-x^2` at x=7?

Answer 1

Slope `m=-14`
equation: `y=-14x+55`

Explanation:

To find the slope you need to derive your function and evaluate the derivative at `x=7`:
deriving:
`y'=-2x`

at `x=7`
`y'(7)=-14`

To find the equation of the tangent line you need also the value of `y` at `x=7`; by substituting into your function:
`y(7)=6-49=-43`
So basically your tangent has solpe `m=-14` and passes through `x_0=7` and `y_0=-43`;
Now use the relationship:
`y-y_0=m(x-x_0)` to find the equation of your line:
`y+43=-14(x-7)`
`y=-14x+55`

Graphicall (the red line is the tangent):