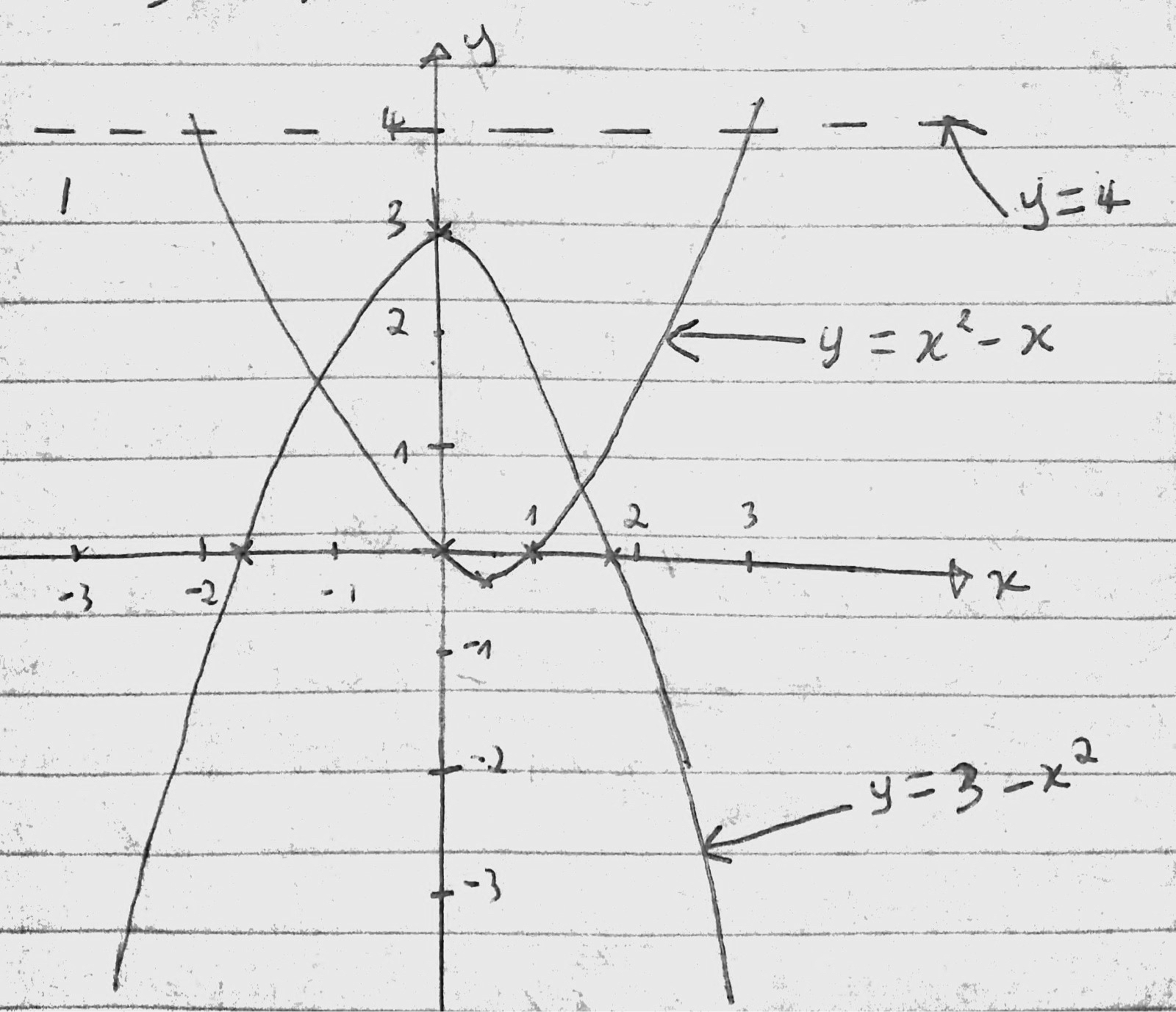
First, sketch the graphs.
#y_1=x^2-x#
#y_2=3-x^2#
#x#-intercept
#y_1=0=> x^2-x=0# And we have that #{(x=0),(x=1):}#
So intercepts are #(0,0)# and #(1,0)#
Get the vertex:
#y_1=x^2-x=>y_1=(x-1/2)^2-1/4=>y_1-(-1/4)=(x-1/2)^2#
So vertex is at #(1/2,-1/4)#
Repeat previous:
#y_2=0=> 3-x^2=0# And we have that #{(x=sqrt(3)),(x=-sqrt(3)):}#
So intercepts are #(sqrt(3),0)# and #(-sqrt(3),0)#
#y_2=3-x^2=>y_2-3=-x^2#
So vertex is at #(0,3)#
Result:
How to get the volume? We shall use the disc method!
This method is simply that: #"Volume"=piint_a^by^2dx#
The idea is simple, however you've got to use it smartly.
And that's what we're going to do.
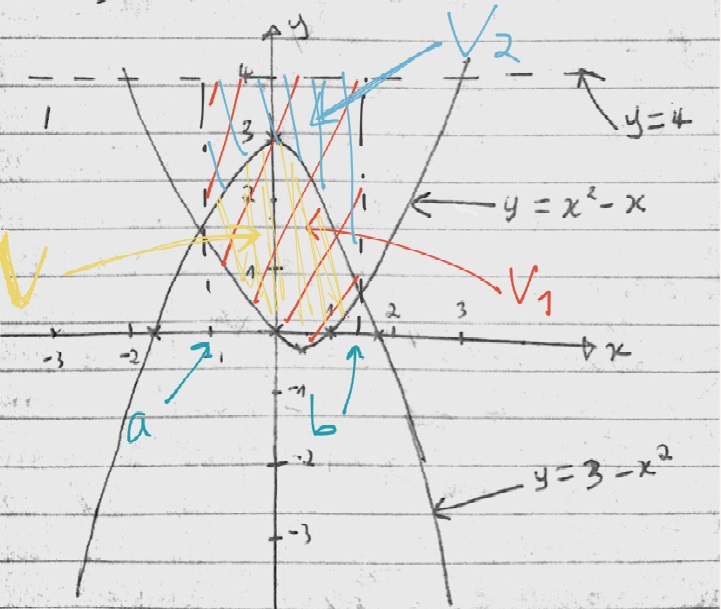
Lets call our volume #V#
#=>V=V_1-V_2#
#V_1=piint_a^b(4-y_1)^2dx#
#V_2=piint_a^b(4-y_2)^2dx#
NB: I'm taking #(4-y)# because #y# is only the distance from the #x#-axis to the curve, whereas we want the distance from the line #y=4# to the curve!
Now to find #a# and #b#, we equate #y_1# and #y_2# and then solve for #x#
#y_1=y_2=> 2x^2-x+3=0#
#=>2x^2+2x-3x+3=0#
#=>(2x-3)(x+1)=0=>{(x=3/2=1.5),(x=-1):}#
Since #a# comes before #b#, #=>a=-1# and #b=1.5#
#=>V_1=piint_(-1)^(1.5)(4-y_1)^2dx=pi int_-1^1.5(4-x^2-x)^2dx= piint_(-1)^(1.5)(x^2+x-4)^2dx#
#=>piint(-1)^(1.5)(x^4+3x^3-7x^2-8x+16)dx=pi[x^5/5+x^4/2-(7x^3)/3-4x^2+16x]_-1^1.5#
#V_1=(685pi)/24#
Do same for #V_2#:
#V_2=piint_-1^1.5(4-y_2)^2dx= piint_-1^1.5(4-3+x^2)^2dx= piint_(-1)^(1.5)(1+x-4)^2dx#
#=>piint(-1)^(1.5)(1+2x^2+x^4)dx=pi[x+(2x^3)/3+x^5/5]_-1^1.5#
#V_1=(685pi)/96#
#V=V_1-V_2=685/24-685/96=color(blue)((685pi)/32)#



