Question

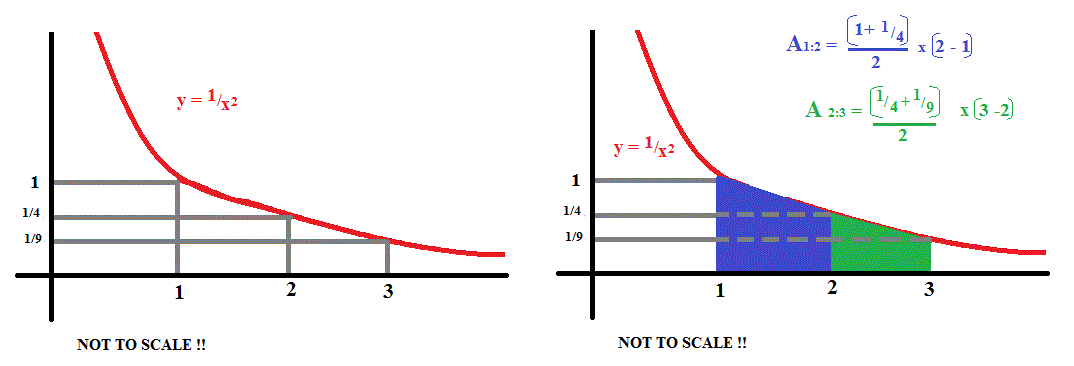
How do you use the trapezoidal rule with n=2 to approximate the area under the curve `y=1/x^2` from 1 to 3?

Answer 1

Draw 2 trapezoids under the curve, the first between `x=1` and `x=2` and the second between `x=2` and `x=3`; use the sum of the areas to approximate the required area.

Explanation:

With `n=2` we have 2 trapezoids
The first will have a width of `1` (the distance on the X-axis between 1 and 2)
and an average height of `(1/1^2 + 1/2^2)/2 = 5/8`

The second will also have a width of `1` (the distance between 2 and 3)
and will have an average height of `(1/2^2+1/3^2)/2 = 13/36`

The total area of the two trapezoids (approximating the area under the curve) is
`color(white)("XXXX")` `5/8 + 13/36 = (45+26)/72 = 71/72`