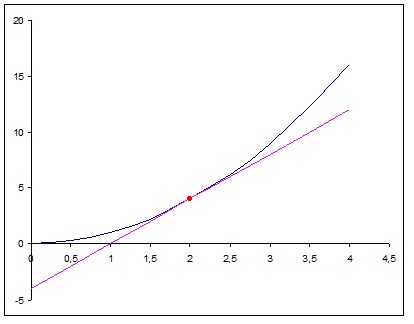
How do you find the equation of the line tangent to the graph of y=x^2 at x=2?
1 Answer
Jul 27, 2015
I found:
Explanation:
First you need the slope
so
now you can use the relationship:
Graphically: