Question

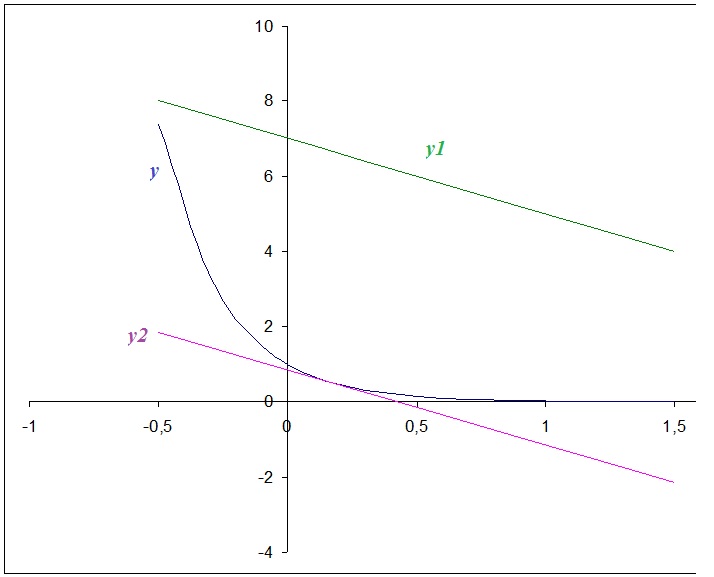
For the curve `y=e^(-4x)`, how do you find the tangent line parallel to the line `2x+y=7`?

Answer 1

I found: `y=-2x-1/2[ln(1/2)-1]`

Explanation:

The tangent line will have slope equal to the derivative of your function:
`y'=-4e^(-4x)`
but it has to be parallel to the line `2x+y=7` or `y=-2x+7` which has slope `=-2`;
So the two slopes must be equal:
`-4e^(-4x)=-2`
`e^(-4x)=1/2`
`-4x=ln(1/2)`
`x=-1/4ln(1/2)`
`x=0.173`
so this is the `x` coordinate of the tangence point the other being:
`y=e^(-4ln(1/2)/-4)=1/2`
So your tangent line has slope `m=-2` and passes therough:
`x_0=-1/4ln(1/2)`
`y_0=1/2`
The equation of this line will be:
`y-y_0=m(x-x_0)`
`y-1/2=-2[x+1/4ln(1/2)]`
`y=-2x-1/2ln(1/2)+1/2`
`y=-2x-1/2[ln(1/2)-1]`

Graphically:
with:
`y=e^(-4x)`
`y1=-2x+7` (the given line) and:
`y2=-2x-1/2(ln(1/2)-1)`