Method 1 (Substitution): One way to solve this is to take the first equation of the system, #x-4y=6#, and solve it for #x# in terms of #y# to get #x=4y+6#. Then plug this into the second equation to make #3x+4y=10# become #3(4y+6)+4y=10#, which simplifies to #12y+18+4y=10#, then #16y=-8#, then #y=-1/2#.
Now use the equation #x=4y+6# to find #x#: #x=4*(-1/2)+6=-2+6=4#.
The answer is the point #(x,y)=(4,-1/2)#.
(BTW, all this work implies the only possible solution is #(x,y)=(4,-1/2)# (so if it is a solution, it is unique). You can confirm it truly is a solution by substitution back into the original system (checking your work proves it is a solution).)
Method 2 (Elimination): Notice that the #-4y# in the first equation and the #4y# in the second equation will cancel if we add the two equations. Do so to get: #4x=16# so #x=4#. Then substitute this into either of the original equations to get, for instance #4-4y=6# so #4y=-2# and #y=-1/2#, resulting in #(x,y)=(4,-1/2)#.
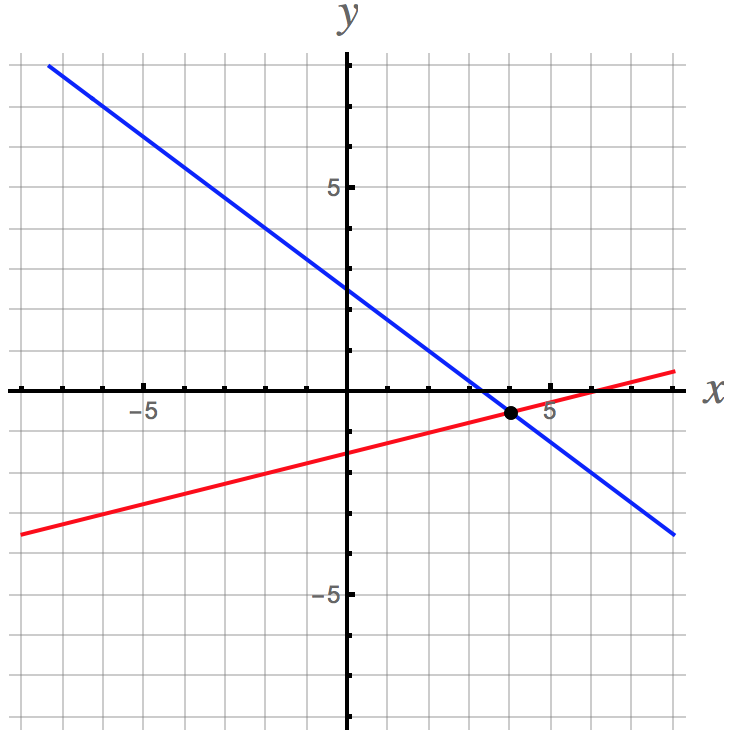
A picture of this situation is shown below. The equation #x-4y=6# is equivalent to #y=1/4 x-3/2# and is the red line with a slope of #1/4# and a #y#-intercept of #-3/2#. The equation #3x+4y=10# is equivalent to #y=-3/4x+5/2# and is the blue line with a slope of #-3/4# and a #y#-intercept of #5/2#.