How do you find the volume of the solid obtained by rotating the region bounded by the curves y=x, x=0, and y=(x^2)-6 rotated around the y=3?
1 Answer
Aug 2, 2015
Explanation:
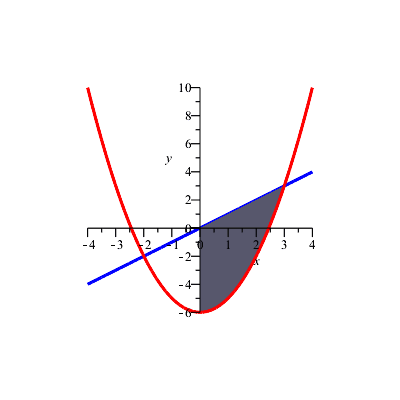
The grey region is what we will be rotating around the horizontal line
The outer radius is
The inner radius is
Using the method of washers
Integrating

