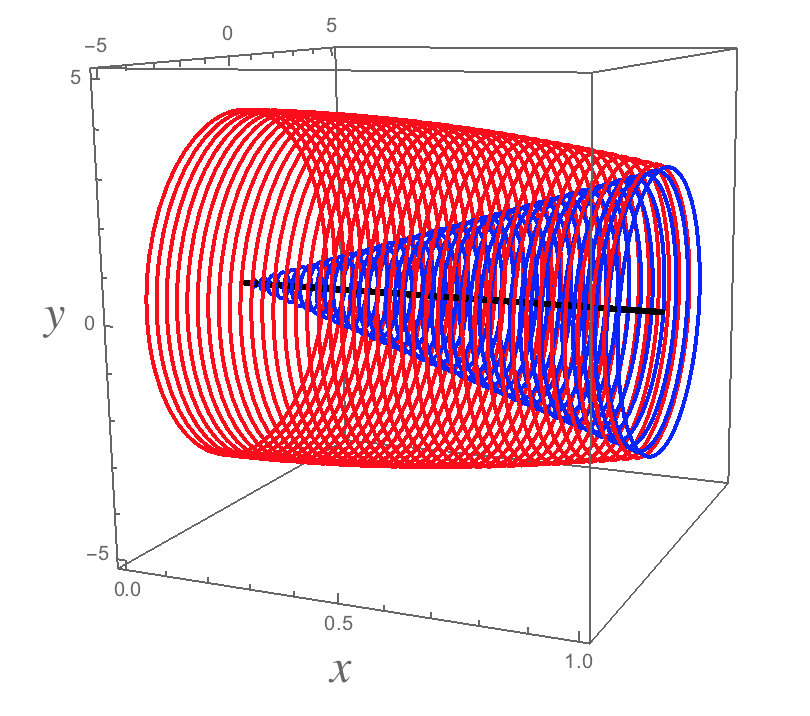
The cross-sections (head on views of vertical slices) for this solid of revolution will be "washers" (the more official name is annuli). The areas of the cross-sections will be given by #pi r_{o}^{2}-pi r_{i}^{2}#, where #r_{i}# is the inner radius and #r_{o}# is the outer radius.
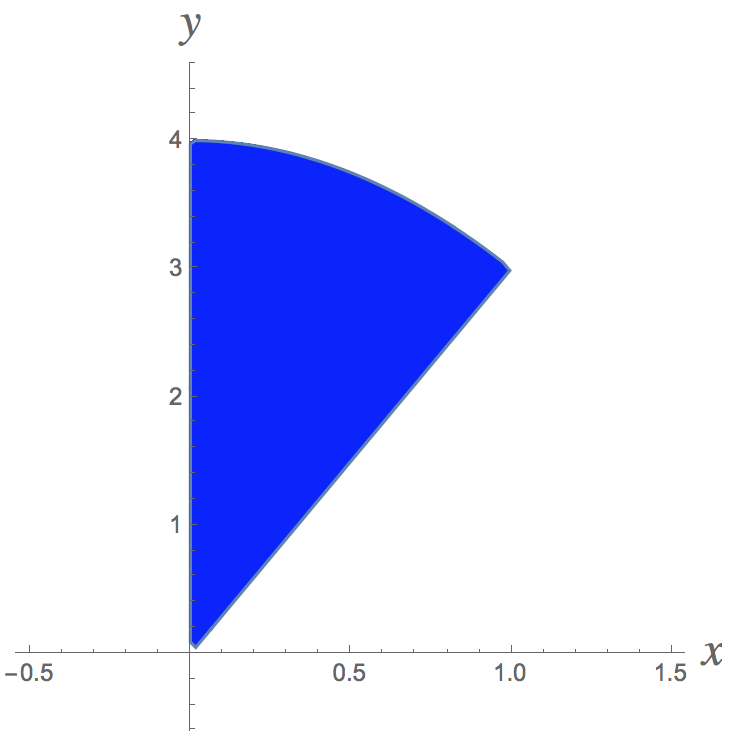
Based on a picture of the region you are revolving around the #x#-axis, the inner and outer radii are the following functions of #x#: #r_{i}=3x# and #r_{o}=4-x^2#.
Therefore, the cross-sectional area, as a function of #x#, is
#A(x)=pi((4-x^2)^2-(3x)^2)=pi(16-17x^2+x^4)#
The volume of the resulting solid is given as a definite integral of #A(x)# over an appropriate interval. Looking at your picture, the lower limit of the integral should be #x=0#. To find the upper limit, solve #4-x^2=3x# to get #x^2+3x-4=0# so #(x+4)(x-1)=0#, which has #x=1# as its only positive root, making that the upper limit of the integral.
Hence
#V=int_{0}^{1}A(x)\ dx=pi int_{0}^{1}(16-17x^2+x^4)\ dx#
#=pi (16x- 17/3 x^3+ 1/5 x^5)|_{0}^{1}=pi(16-17/3+1/5)#
#=pi((240-85+3)/15)=(158pi)/15#
Here's a picture of the 2-dimensional region that gets revolved around the #x#-axis:
And here's a picture of the 3-dimensional solid (with a different scale on the #x#-axis so it looks more stretched out). The solid itself is the part "between" the red and the blue (BTW, I made the sides of the solid out of circles with space between them just so you could see inside the solid...in reality, the space between the circles is part of the sides of the solid as well).