How do you use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region #x+y=6# and #x=7-(y-1)^2# rotated about the x-axis?

Question

1907 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-08-15T02:47:52

#(27pi)/2#

Since we are revolving the around the x axis using the shell method we will be integrating with respect to y.

To proceed we need to find where the functions intersect

Solve #x+y=6# for #x#

#x=6-y#

Now set the two functions equal to each other

#6-y=7-(y-1)^2#

#6-y=7-(y^2-2y+1)#

#6-y=7-y^2+2y-1#

#6-y=6-y^2+2y#

#-y=-y^2+2y#

#y^2-y-2y=0#

#y^2-3y=0#

#y(y-3)=0#

#y=0# and #y=3#

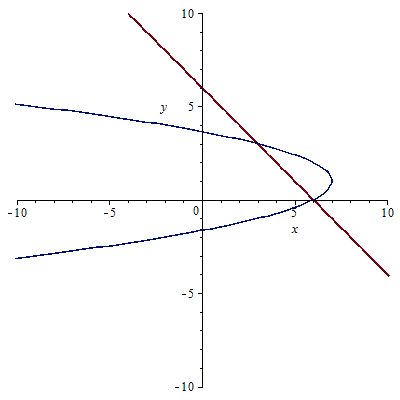
enter image source here

Our radius will be some value #y# over the interval
#0<=y<=3#

Our cylinder height is
#7-(y-1)^2-(6-y)#

The integral for the volume is

#2piint_0^3y[7-(y-1)^2-(6-y)]dy#

#2piint_0^3y[7-(y^2-2y+1)-(6-y)dy#

#2piint_0^3y[7-y^2+2y-1-6+y]dy#

#2piint_0^3y[-y^2+3y]dy#

#2piint_0^3-y^3+3y^2dy#

Integrating we have

#2pi[-y^4/4+y^3]#

Now evaluating we get

#2pi[-(3)^4/4+3^3]=2pi[-81/4+27]#

#2pi[-81/4+108/4]=2pi[27/4]=(27pi)/2#