What uses do products of power series have?
1 Answer
One example that I find useful is the use and manipulation of the products of power series to derive
What is accepted by Physical Chemists is that you can write out the general solution to the Equation as:
#y(x) = c_1 e^(alphax) + c_2 e^(-alphax)#
where
#psi(x) = sum_(i=1)^N c_i phi_i(x)#
where each#phi# could, for example, represent an atomic orbital, and#psi(x)# would in that case be the molecular orbital.
A common example of solving the time-dependent Schroedinger equation is (example 2-4 in Physical Chemistry: A Molecular Approach):
#(d^2x(t))/(dt^2) + omega^2x(t) = 0#
subject to the boundary conditions
To solve this one, one would have to use identity written at the top, with
#c_1e^(alphax) + c_2e^(-alphax)#
#= c_1(cosx + alphasinx) + c_2(cosx - alphasinx)#
#= c_1cosx + c_1alphasinx + c_2cosx - c_2alphasinx#
#= (c_1 + c_2)cosx + (c_1alpha - c_2alpha)sinx#
and it is generally written out by absorbing the arbitrary constants
#= c_3cosx + c_4sinx#
Then, substituting
#c_3cos(omegat) + c_4sin(omegat)#
for the solution to the so-called common example.
Looking at the boundary condition
#= c_3(-sin(omegat))*omega + c_4cos(omegat)*omega#
#= cancel(c_3(-sin(omega(0)))*omega)^(0) + c_4cos(omega(0))*omega#
#= c_4omega#
But we know that at
#=> c_4omega = 0# , thus satisfying the condition#(dx(0))/(dt) = 0# .
Using the
#x(0) = c_3cos(omega(0)) + cancel(c_4sin(omega(0)))^(0)#
#= c_3#
with
#color(blue)(x(t) = Acos(wt))#
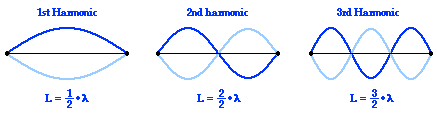
which is the familiar physics equation for a transverse wave, as depicted in the image above! :)

